Метод интегрирования подведением под знак дифференциала

Функция 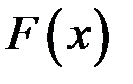называется первообразной для функции 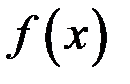на интервале 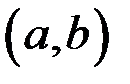, конечном или бесконечном, если в любой точке 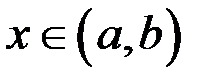этого интервала функция дифференцируема и имеет производную .

Совокупность всех первообразных для функции , определенных на интервале , называется неопределенным интегралом от функции на этом интервале и обозначается символом

.

Метод подведения под знак дифференциала следует из свойства инвариантности неопределенного интеграла.

Пусть дан интеграл .Справедливо равенство

,

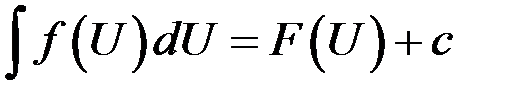где 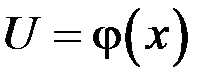– некоторая непрерывно дифференцируемая функция.

Таблица интегралов

1.	8.
2.	9.
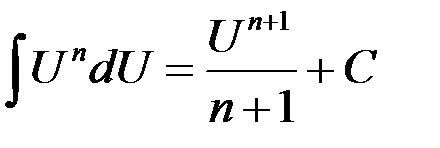
3.	10.
4.	11.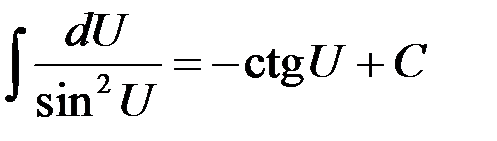
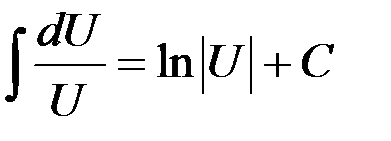
5.	12.
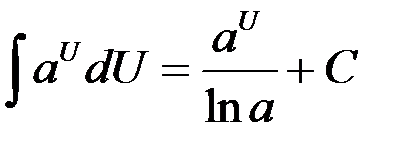
6.	13.
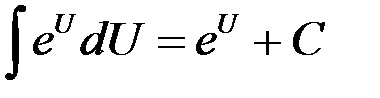
7.	14.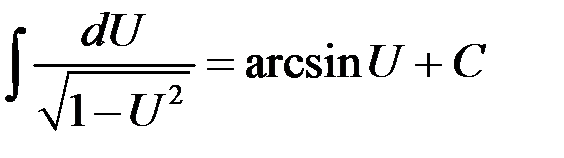
15.

При интегрировании методом подведения под знак дифференциала необходимо иметь в виду следующие равенства:

В общем случае

.

Пример 1

Найти интеграл .

Так как , то

.

Пример 2

Найти интеграл .

Так как , то

.

Пример 3

Найти интеграл .

Так как 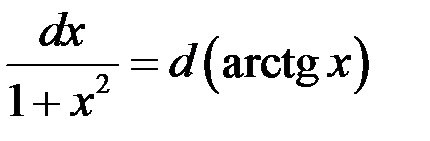, то

Пример 4

Найти интеграл .

Так как , то

.

Не нашли, что искали? Воспользуйтесь поиском: