Вычисление площадей с помощью определенного интеграла

Пусть функция определена и непрерывная на отрезке и пусть, для определенности,

Разобьем отрезок на n частей произвольным образом точками деления: .Выберем на каждом частичном промежутке произвольным образом точки .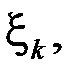

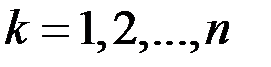Обозначим Составим сумму , которая называется интегральной суммой для функции на отрезке .

Обозначим длину наибольшего частичного промежутка через 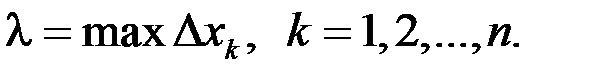Перейдем к пределу при .

Если существует конечный предел , не зависящий от способа разбиения отрезка на частичные и выбора на них точек , то он и называется определенным интегралом от функции на отрезке и обозначается

Если – любая первообразная для функции , то справедлива формулаНьютона – Лейбница:

,

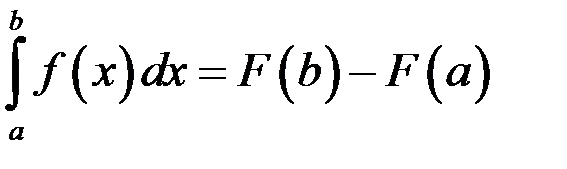т.е. для вычисления определенного интеграла от непрерывной функции нужно составить разность значений произвольной ее первообразной для верхнего и нижнего пределов интегрирования.

Пример 1

Если то численно равен площадикриволинейной трапеции, ограниченной кривой ,

прямыми 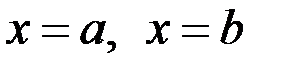и осью ох:

Если меняет знак конечное число раз на отрезке , то интеграл по всему отрезку разбивается на сумму интегралов по частичным отрезкам, интеграл будет положителен там, где и отрицателен, где :

.

Пусть нужно вычислить площадь фигуры, ограниченной кривым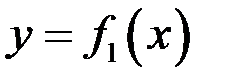и и и прямыми , тогда при условии имеем

Пример 2

Вычислить площадь фигуры, ограниченной линиями и .

Решение

у у=х+ 3     у=х 2+1 3       –3 –1 0 2 х

Найдем точки пересечения: ,

.

Тема № 5

Не нашли, что искали? Воспользуйтесь поиском: