Оценка точности технологического процесса.

В процессе механической обработки заготовки, любым технологическим процессом, на точность её изготовления влияет достаточно большое количество различных факторов. Так, например, при обработке деталей на станке участвуют станок, приспособление для установки и закрепления деталей и режущего инструмента, режущий инструмент, сами обрабатываемые детали, настройщик оборудования, окружающая среда и т.д. В силу действия различных производственных факторов непрерывно меняются и показатели конечного результата выбранного технологического процесса.

Несмотря на то, что детали изготавливают при помощи одного и того же технологического процесса, при постоянных режимах обработки и в автоматическом режиме, т.е без участия человека, все они отличаются друг от друга и от расчётного «идеального» прототипа. Такое явление называется рассеиванием случайной величины, в частности точности изготовления выходных параметров детали.

Для анализа точности изготовления деталей, выбранным технологическим процессом, применяются различные методы, позволяющие учитывать влияние различных производственных факторов. К таким методам относятся: метод непосредственного наблюдения или метод точечных диаграмм, аналитический и статистический методы.

В производстве наиболее часто применяется метод точечных диаграмм, который позволяет определить влияние закономерно изменяющихся факторов на точность изготовления. Метод требует достаточно большого количества наблюдений и применяется в крупносерийном производстве.

Аналитический метод требует математического описания всех первичных факторов влияющих на погрешность обработки, метод достаточно трудоёмкий и применяется в отдельных случаях.

Статистический метод основан на положениях теории вероятности и математической статистики. Из теории вероятностей известно, что если рассеяние какой либо величины (размера, шероховатостей поверхности, твёрдости материала и т.д.) зависит от совокупного действия многих факторов одного порядка величин, являющихся случайными, независящими или слабо зависящими один о другого, то рассеяние подчиняется закону нормального распределения или закону Гаусса.

Теоретический закон нормального распределения в системе координат, в которой начало совпадает с осью симметрии кривой Рис. 2.2 или со средним значением отклонения, выражается формулой

Y = j(х) = е ^- (2)

где - средне квадратичное отклонение случайной величины;

- частота, отвечающая значению х.

Для анализа точности выбранного технологического процесса производят измерение фактических размеров партии деталей и строят кривую распределения.

Разность между минимальным и максимальным фактическими размерами

измеренных деталей разбивают на равные интервалы.

Определяют количество размеровдеталей в каждом Рис.2.2

интервале.

Построение кривой производят в следующей последовательности. По оси абсцисс откладывают поле рассеивания размеров, которое определяется как разность между фактическим максимальным и минимальным размерами Х_ф.мах – Х_ф.мин. = 6 , в выбранном масштабе. Из середины каждого интервала, по оси ординат, откладывают относительную частоту W = m /N, где m– количество размеров деталей попавших в данный интервал, N – общее количество деталей в измеряемой партии. По полученным точкам строят ломанную кривую фактического распределения размеров.Чем больше партия деталей тем плавнее становится ломанная кривая, и по своему виду приближается к кривой закона нормального распределения (кривой Гаусса) Рис.2.3.На графике обозначения X_{д min}и Х_д.max определяют допустимые max и min значения контролируемого размера или границы допуска, величина заданная конструктором. Области А _i и Б _i соответствуют величине исправимого и неисправимого брака, а величина а _i определяет смещение центра группирования размеров относительно середины поля допуска. Кривая нормального распределения симметрична относительно оси, соответствующей абсциссе М(х) или Х_СР, среднеарифметическое значение отклонений. Среднеарифметическое значение отклонений называют центром группирования размеров или центром рассеяния случайной величины.

Рис.2.3

Теоретическая кривая нормального рассеяния размеров простирается в обе стороны вдоль оси абсцисс беспредельно, асимптотически приближаясь к этой оси. Для теоретических расчётов предельных отклонений (при использовании закона нормального рассеяния), выражаемые в долях среднеквадратичного отклонения , ограничивают обычно величинами 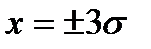или полем рассеивания 6 .

Площадь под кривой закона нормального распределения, находящаяся в

в зоне ограниченной 6 , составляет 99,73% от всей площади и только 0,27% выходят за пределы поля рассеивания.

Если всю площадь под кривой нормального распределения принять за 100% или за единицу, то её незаштрихованная площадь будет соответствовать доле отклонений случайной величины, которая укладывается в интервал .

При увеличении интервала рассеивания более 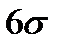площадь под кривой увеличивается незначительно, при уменьшении до площадь под кривой резко

сокращается.

Характер рассеивания размеров наиболее наглядно выявляется путем составления так называемых кривых распределения. Для получения надежной кривой распределения рекомендуется получить не менее 200 – 300 замеров фактических величин данного размера, во многих случаях, однако, практически допустимые результаты могут быть получены при числе замеров около 100.

Количество деталей, подлежащих измерению для определения среднеквадратичного отклонения, зависит от точности, с которой необходимо определить это отклонение.

Из математической статистики известно, что среднеквадратичная ошибка при определении среднеквадратичного значения равна:

(.3)

где N – количество измерений, а Е – ошибка в долях от .

Для получения с точностью 5%, надо решить уравнение

, откуда N 200.

Для определения среднеквадратичного отклонения с точностью 10%, надо измерить 50 деталей.Вид кривой фактического распределения зависит от рассматриваемого технологического процесса изготовления, количества деталей подвергаемых измерениям и ряда других факторов.

Разница между предельными размерами деталей данной партии, «поле рассеивания» - характеризует величину случайных погрешностей. Систематическая погрешность, постоянная в пределах партии, на форму кривой распределения влияния не оказывает – она вызывает лишь смещение всей кривой в направлении оси абсцисс.

В случае, если на точность изготовления влияют закономерно изменяющиеся производственные факторы, то кривая нормального распределения будет несимметрична относительно центра группирования. Построение и исследование кривых распределения для различных операций позволяют сделать ряд выводов, относящихся к точности обработки; и в первую очередь дают возможность отделять влияние постоянных систематических ошибок от влияния ошибок случайных.

Далее те же исследования позволяют в ряде случаев предсказывать значение случайных погрешностей, основываясь на обследованной ранее партии деталей. Ряд работ по исследованию кривых распределения размеров деталей показывает

близкое совпадение фактических кривых распределения с кривой нормального распределения, уравнение которой имеет вид:

(.4)

где х_i – текущие координаты кривой,

Х - средняя арифметическая из всех величин,

(.5)

здесь … m_n - число деталей с отклонениями, х₁,х_2….х_n

- среднее квадратное отклонение размеров, определяется по формуле

(.6)

или

(.7)

В формулах (6 и7)N – общее число измеренных деталей, а

m – число деталей с одинаковым отклонением размеров.

Если фактическое распределение размеров (или отклонений) практически

Рис.2.4

близко подходит к закону нормального распределения, то оно может быть достаточно полно охарактеризовано величиной среднего квадратичного отклонения. Отсюда может быть выведено обязательное неравенство, связывающее величину допуска на данный размер () и величину среднего квадратичного отклонения: .

(8)

На Рис.2.4. приведён случай, когда поле допуска равно полю рассеивания размеров, при отсутствии систематической погрешности, вызванной неправильной настройкой станка.

Для получения требуемых размеров детали, в процессе механической обработки, настройка станка производится с расчетом получения центра группирования () в середине поля допуска. На практике возможны различные варианты влияния случайных факторов на характер расположения и величину поля рассеивания относительно поля допуска. В частности, на Рис.2.5 и Рис.2.6 приведены случаи, когда центр группирования совпадает с серединой поля

Рис.2.5 Рис.2.6

допуска, а или 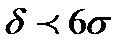. В первом случае все детали соответствуют требованиям точности изготовления. Во втором случае появляется брак, как исправимый А _{i ,} таки неисправимый Б _i. Для исключения возможности появления брака необходимо изменить технологический процесс обработки, и в частности, поменять режимы обработки или использовать более высокоточное оборудование.

В случае, если настройка станка, на выполнение заданного размера, произведена с погрешностью а _i, а величина Рис.2.7 или Рис.2.8, то появляется брак исправимый или неисправимый, или тот и другой одновременно.

Величина брака зависит как от величины систематической погрешности, так и от выбранного технологического процесса изготовления.

Рис.2.7 Рис.2.8

Величина систематической погрешности а _i определится по формуле

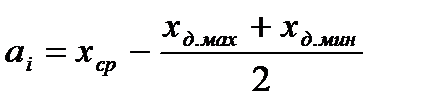(9)

Величина брака или количество отклонений, выходящих за границы поля допуска определится по формулам.

Площадь А А_i = 0,5 [1 – Ф(t_a)] где t_{a =} (10)

Площадь Б Б_i = 0,5 [1- Ф(t_б)} где t_{б =} (11)

В формулах (10 и 11) Ф(t) обозначает табулированную функцию Лапласа значение которой определяется по таблицам приводимым почти а каждом курсе теории вероятностей или математической статистики. Определив t_a и t_б и взяв их величину из соответствующих таблиц, легко найти значение Ф(t). Подставляя полученные значения в формулы, определим вероятность возникновения брака (заштрихованные площадки А_i и Б_i) выраженного в долях от площади под кривой нормального распределения. Умножив полученное значение на 100% определим процент появления брака в контролируемой партии деталей.

Не нашли, что искали? Воспользуйтесь поиском: