Закон Джоуля-Ленца.

Рассмотрим однородный проводник, к концам которого приложено напряжение U. За время 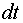через сечение проводника переносится заряд . Так как ток представляет собой перемещение заряда под действием электрического поля, то работа тока

. (7.13)

Соответственно мощность, выделяемая в цепи, определяется по формуле

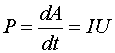. (7.14)

Энергия, выделяемая в цепи постоянного тока, может расходоваться:

– на выделение теплоты (например, спираль электроплиты при пропускании тока нагревается);

– совершение механической работы (например, ротор электродвигателя при протекании по нему тока вращается);

– совершение химических превращений (например, при зарядке аккумулятора);

– свечение (например, лампы дневного света при подаче на них напряжения);

– генерацию акустических волн (например, в электродинамиках) и т. д.

В случае, когда проводник неподвижен и химических превращений в нем не совершается, работа тока [формула (7.13)] затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается. При протекании тока в проводнике выделяется теплота

.

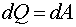Заменив в (7.13) в соответствии с законом Ома , получим формулу

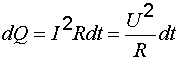. (7.15)

Соотношение (7.15) было установлено экспериментально в 1841 г. английским физиком Д. Джоулем и независимо от него в 1842 г. русским ученым Э. Х. Ленцем и носит название закона Джоуля–Ленца: количество теплоты, выделяющейся в единицу времени на участке цепи, при протекании по нему постоянного тока, равно произведению сопротивления участка цепи на квадрат силы тока.

Поскольку величины, фигурирующие в формуле (7.15), являются интегральными (характеризующими проводник конечных размеров), то можно сказать, что выражение (7.15) описывает закон Джоуля–Ленца в интегральной форме.

От формулы (7.15), определяющей теплоту, выделяющуюся во всем проводнике, можно перейти к выражению, характеризующему выделение теплоты в различных местах проводника. Выделим в проводнике таким же образом, как это было сделано при выводе формулы (7.9), элементарный объем в виде цилиндра (см. рис. 7.1). Согласно закону Джоуля–Ленца за время 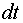в этом объеме выделится теплота

, (7.16)

где – элементарный объем.

Разделив выражение (7.16) на 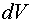и 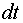, найдем количество теплоты, выделяющееся в единице объема в единицу времени, – удельную тепловую мощность тока:

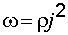. (7.17)

Используя дифференциальную форму закона Ома [формула (7.9)] и соотношение 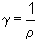, получим

. (7.18)

Формула (7.18) представляет собой дифференциальную форму закона Джоуля–Ленца.

Отметим, что Джоуль и Ленц установили свой закон для однородного участка цепи. Однако, как следует из выкладок, приведенных в данном параграфе, формулы (7.15) и (7.18) справедливы и для неоднородного участка при условии, что действующие в нем сторонние силы имеют нехимическое происхождение.

Не нашли, что искали? Воспользуйтесь поиском: