Закон Ома в дифференциальной и интегральной форме для неоднородного участка цепи

В 1826 г. немецкий физик Г. Ом (1787–1854) экспериментально установил закон, согласно которому, сила тока, проходящего в однородном проводнике, пропорциональна напряжению на концах проводника:

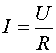, (7.6)

где R – характеристика проводящей среды, электрическое сопротивление проводника. В СИ сопротивление измеряется в омах (Ом).

Значение сопротивления проводника R зависит от материала, из которого проводник изготовлен, а также его размеров и формы. Для однородного проводника с площадью поперечного сечения S и длиной l имеем

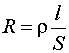, (7.7)

где – удельное электрическое сопротивление проводника.

Закон Ома в виде выражения (7.6) устанавливает соотношение между интегральными величинами (I определяется интегралом (7.2), a U – интегралом (7.5)) и называется законом Ома для однородного участка цепи в интегральной форме.

Рассмотрим малый объем проводящей среды в виде цилиндра сечением S и длиной l (рис. 7.1). Причем будем считать, что в пределах этого объема неоднородностью таких характеристик, как плотность тока j, напряженность электрического поля , можно пренебречь. Чем меньше будет объем цилиндра, тем справедливее будет сделанное допущение. Подставляя выражения (7.2) и (7.7) в формулу (7.6) и учитывая постоянство электрических характеристик в рассматриваемом объеме, получим

,

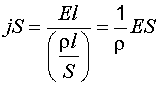, (7.8)

где 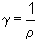– удельная электрическая проводимость проводника. Единицей измерения проводимости в СИ является 1 сименс (1 См).

Учитывая коллинеарность векторов и в однородной проводящей среде (рис. 7.2, а), перепишем (7.8) в виде

. (7.9)

Формула (7.9) описывает закон Ома для однородного участка цепи в дифференциальной форме. Для неоднородного участка цепи (рис. 7.2, б), т. е. при наличии сторонних сил, закон Ома, как это следует из формулы (7.5), принимает следующий вид:

в интегральной форме ( – общее сопротивление проводника и источника тока на участке 1–2)

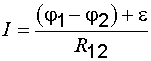; (7.10)

в дифференциальной форме

. (7.11)

Для замкнутой цепи (рис. 7.2, в) справедливо выражение

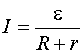, (7.12)

где – суммарная электродвижущая сила в цепи; r – внутреннее сопротивление источников тока; R – внешнее по отношению к источникам сопротивление цепи.

Не нашли, что искали? Воспользуйтесь поиском: