Поток вектора напряженности. Теорема Гаусса

Теорема Гаусса. Элементарным потоком dФ сквозь площадку dS называют величину

dФ = E · dS · cosa = E_n dS = · ,

где E_n - проекция вектора на направление нормали к площадке, - вектор, модуль которого равен dS, а направление совпадает с нормалью . Для произвольной поверхности S поток вектора сквозь нее можно записать:

. (7.7)

Подставив значение Е для точечного заряда, последнюю формулу можно записать:

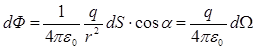, (7.8)

где - телесный угол, опирающийся на элемент поверхности dS с вершиной в точке расположения заряда q. Интегрируя выражение (4.8) по всему телесному углу мы получим .

В случае, когда поле создается системой точечных зарядов q₁, q₂¼ q_n то в соответствии с принципом суперпозиции полей имеем:

Каждый интеграл в правой части равен q_i /e_о, если заряд q_i находится внутри замкнутой поверхности. Поэтому в правой части предыдущего уравнения мы должны записать алгебраическую сумму зарядов q_i, находящихся внутри поверхности S. Таким образом, окончательно можно записать:

. (7.9)

Данное уравнение математически выражает теорему Гаусса: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри данной поверхности, деленной на e₀..

40. Работа, совершаемая при перемещении электростатического поля вдоль замкнутого контура.

Пусть, в поле заряда q помещается заряд q₀, который под действием сил поля заряда начнется перемещаться (рис.7.4). Элементарная работа, совершаемая при этом будет равна: поскольку , , или:

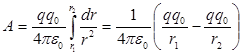. (7.10)

Из (7.10) следует, что работа по перемещению заряда в электростатическом поле не зависит от формы пути перехода, а зависит только от положения начальной и конечной точек перемещения, т.е. электростатическое поле точечного заряда является потенциальным, а электростатические силы консервативными. В случае, когда заряд q₀ перемещается в поле системы зарядов, то на движущийся заряд по принципу суперпозиций действует сила и работа равнодействующей силы равна алгебраической сумме работ соответствующих сил:

, (7.11)

где r_i1 и r_i2 расстояния от заряда q_i до начальной и конечной точки перемещение заряда q₀. Из формулы (7.10) также следует, что работа, совершаемая при перемещении заряда в электростатическом поле по замкнутому пути, равна нулю, т.е. .

Не нашли, что искали? Воспользуйтесь поиском: