Циркуляция вектора напряженности электростатического поля вдоль замкнутого контура.

Работа по перемещению заряда в электростатическом поле не зависит от формы пути перехода, а зависит только от положения начальной и конечной точек перемещения, т.е. электростатическое поле точечного заряда является потенциальным, а электростатические силы консервативными. В случае, когда заряд q₀ перемещается в поле системы зарядов, то на движущийся заряд по принципу суперпозиций действует сила и работа равнодействующей силы равна алгебраической сумме работ соответствующих сил:

, (7.11)

где r_i1 и r_i2 расстояния от заряда q_i до начальной и конечной точки перемещение заряда q₀. Из формулы (7.10) также следует, что работа, совершаемая при перемещении заряда в электростатическом поле по замкнутому пути, равна нулю, т.е. . Если перемещённый заряд принять за единицу, то (7.11) можно записать:

, или . (7.12)

Этот интеграл называется циркуляцией вектора напряженности вдоль замкнутого контура.

Из теоремы о циркуляции вектора напряженности можно сделать несколько важных выводов: 1) линии напряженности поля не могут быть замкнутыми; 2) существование электростатического поля вида, показанного на рис. 7.5 невозможно.

	Рис.7.5
Рис.7.4

В самом деле, если применить к этому полю теорему о циркуляции вектора по замкнутому контуру, показанному на рис. 7.6 пунктиром, то она была бы отлична от нуля, что противоречит теореме.

Вопрос №42

Потенциал электростатического поля. Поскольку работа консервативных сил равна убыли потенциальной энергии, то на основании формулы (7.13) выражение для потенциальной энергии заряда q₂ в поле заряда q₁ можно записать в виде

. (7.16)

Как видно из выражения (7.16), Wp определяется с точностью до постоянной величины. В данном случае для электрического поля точечного заряда принято выбирать const так, чтобы на бесконечно большом расстоянии между зарядами их взаимная потенциальная энергия обращалась в нуль: r → ∞, Wp = 0. Следовательно,

. (7.17)

Из формулы (7.17) следует, что отношение W/q₂ для данной точки поля не зависит от величины заряда q₂. Поэтому это отношение может служить энергетической характеристикой электростатического поля, которая называется потенциалом поля,и равна отношению потенциальной энергии пробного заряда, помещенного в данную точку поля, к величине этого заряда

. (7.18)

Из выражений (7.17) и (7.18) следует, что потенциал поля точечного заряда q равен

[В]. (7.19)

Работа по перемещению заряда в электростатическом поле равна произведению величины заряда на разность потенциалов в начальной и конечной точке перемещения

. (7.20)

Если поле создаётся системой зарядов q₁, q₂, …q_n, то для потенциальной энергии заряда q_пр в поле системы зарядов получим

. (7.21)

С учетом (7.19), потенциал поля системы зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности

(7.22)

7.7 Связь между потенциалом j и напряжённостью электрического поля . Дифференциальную формулу связи и φ, справедливую для малой окрестности какой-либо точки поля, можно вывести из выражений для элементарной работы . Откуда

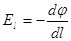, (7.18)

где E_l – проекция вектора на направление в пространстве.

В более общем векторном виде вектор равен , где

– единичные векторы, направленные соответственно вдоль осей х, у, z Последнее уравнение можно записать в виде

или Ñj, (7.19)

т.е. напряжённость поля равна градиенту потенциала и направлена в сторону убывания потенциала.

Вопрос №43

7.8 проводники в электрическом поле. Если проводнику сообщить некоторый заряд или его поместить во внешнее электростатическое поле, то в обоих случаях на заряды проводника будет действовать электростатическое поле и они будут перемещаться внутри проводника. Этот процесс будет происходить до тех пор, пока внутри проводника поле не будет равно нулю и потенциал внутри проводника должен быть постоянным (j=const). Напряженность на поверхности проводника в каждой точке должна быть направлена по нормали. В противном случае касательные составляющие привели бы заряды, находящиеся на поверхности в движение, и равновесие зарядов было бы нарушено. Применив теорему Гаусса, можно определить напряжённость поля непосредственно у поверхности проводника

,

где e – диэлектрическая проницаемость среды, окружающей проводник, s – поверхностная плотность заряда.

7.9 Электроемкость уединенного проводника. Рассмотрим проводник, удаленный от других проводников, тел и зарядов в связи с чем его можно рассматривать как уединенный проводник. Из опыта следует, что между зарядом и потенциалом существует зависимость q = Сj.

Величину называют электроемкостью или просто емкостью уединенного проводника. Емкость зависит от формы и размеров проводника и не зависит от материала, агрегатного состояния и от размеров полостей внутри проводника. Емкость не зависит от заряда и потенциала проводника.

7.10 Электроемкость конденсаторов. Система проводников, близко расположенных друг другу и заряженных одинаковыми по величине, но противоположными по знаку зарядами называется конденсатором, а проводники – его обкладками. Емкость конденсатора определяется

,

где j₁ - j₂ –разность потенциалов между обкладками, q – заряд, расположенный на положительно заряженной обкладке конденсатора. По форме обкладок конденсаторы бывают плоские, цилиндрические и сферические:

1) электроёмкость плоского конденсатора

, (7.22)

2) электроёмкость цилиндрического конденсатора

, (7.23)

где – длина конденсатора, R₁ и R₂ – радиусы внутренней и наружной цилиндрических обкладок.

3) Электроемкость сферического конденсатора

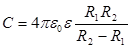, (7.24)

где R₁ и R₂ – радиусы внутренней и наружной обкладок.

Вопрос №44

7.11 Энергия заряженного конденсатора. Процесс зарядки конденсатора можно представить как последовательное перемещение бесконечно малых порций заряда dq с одной пластины на другую, в результате чего одна из пластин будет заряжаться положительно, а другая – отрицательно и между ними будет возникать постепенно возрастающая разность потенциалов U = q / С. При этом энергия конденсатора равна

.

Здесь Е – напряженность электрического поля внутри конденсатора, a V= S d –его объем. Отсюда энергия единицы объема, или объемная плотность энергии электрического поля

В изотропном диэлектрике направления векторов и совпадают. Поэтому формуле для плотности энергии можно придать вид

.

Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика.

7.6 Потенциал электростатического поля. Поскольку работа консервативных сил равна убыли потенциальной энергии, то на основании формулы (7.13) выражение для потенциальной энергии заряда q₂ в поле заряда q₁ можно записать в виде

. (7.16)

Как видно из выражения (7.16), Wp определяется с точностью до постоянной величины. В данном случае для электрического поля точечного заряда принято выбирать const так, чтобы на бесконечно большом расстоянии между зарядами их взаимная потенциальная энергия обращалась в нуль: r → ∞, Wp = 0. Следовательно,

.

Из формулы (7.17) следует, что отношение W/q₂ для данной точки поля не зависит от величины заряда q₂. Поэтому это отношение может служить энергетической характеристикой электростатического поля, которая называется потенциалом поля,и равна отношению потенциальной энергии пробного заряда, помещенного в данную точку поля, к величине этого заряда

.

Из выражений (7.17) и (7.18) следует, что потенциал поля точечного заряда q равен

[В].

Работа по перемещению заряда в электростатическом поле равна произведению величины заряда на разность потенциалов в начальной и конечной точке перемещения

.

Не нашли, что искали? Воспользуйтесь поиском: