
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Реальные газы, Уравнение Ван-дер-Вальса
Уравнение Ван-дер-Ваальса
В уравнении, описывающем состояние реального газа, должны быть учтены объём молекул и силы межмолекулярного взаимодействия. Поэтому голландским физиком Ван-дер-Ваальсом были внесены две поправки в уравнение состояния идеального газа. Рассмотрим их.
11.1 Учёт собственного объёма молекул
При сближении частиц возрастают силы отталкивания. Они противодействуют взаимному проникновению молекул в занятые ими пространства. Поэтому свободный объём, в котором могут двигаться молекулы реального газа, должен быть уменьшен на величину  , пропорциональную их собственному объёму. Следовательно, вместо величины
, пропорциональную их собственному объёму. Следовательно, вместо величины  в уравнении состояния следует поставить величину
в уравнении состояния следует поставить величину
(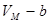 ). (11.1)
). (11.1)
Постоянная  должна быть больше суммарного объёма всех молекул газа, т. к. даже при плотной «укладке» молекул-шариков между ними остаются незаполненные промежутки.
должна быть больше суммарного объёма всех молекул газа, т. к. даже при плотной «укладке» молекул-шариков между ними остаются незаполненные промежутки.
11.2 Учёт притяжения молекул
Силы взаимного притяжения молекул приводят к появлению дополнительного давления на газ, называемого внутренним давлением  . Поэтому в уравнении состояния давление
. Поэтому в уравнении состояния давление  следует заменить величиной (
следует заменить величиной ( ). По вычислениям Ван-дер-Ваальса внутреннее давление пропорционально квадрату концентрации молекул или обратно пропорционально квадрату молярного объёма газа (
). По вычислениям Ван-дер-Ваальса внутреннее давление пропорционально квадрату концентрации молекул или обратно пропорционально квадрату молярного объёма газа ( )
)
 , (11.2)
, (11.2)
где  – постоянная величина, зависящая от природы газа. Введя обе поправки в уравнение Клапейрона, получим уравнение состояния одного моля реального газа (уравнение Ван-дер-Ваальса):
– постоянная величина, зависящая от природы газа. Введя обе поправки в уравнение Клапейрона, получим уравнение состояния одного моля реального газа (уравнение Ван-дер-Ваальса):
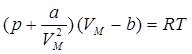 . (11.3)
. (11.3)
Для произвольного количества 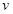 газа (
газа ( ) можно записать
) можно записать
 , (11.4)
, (11.4)
где  и
и  – постоянные величины, определяемые экспериментально;
– постоянные величины, определяемые экспериментально;  – объём, занимаемый газом. Уравнение Ван-дер-Ваальса также является приближённым, т. к. при его выводе был сделан целый ряд упрощений. Это не единственное уравнение, описывающее реальные газы. Существуют и другие, но они не рассматриваются из-за их сложности.
– объём, занимаемый газом. Уравнение Ван-дер-Ваальса также является приближённым, т. к. при его выводе был сделан целый ряд упрощений. Это не единственное уравнение, описывающее реальные газы. Существуют и другие, но они не рассматриваются из-за их сложности.
11.3 Изотермы Ван-дер-Ваальса и их анализ
Уравнение Ван-дер-Ваальса является уравнением третьей степени относительно объёма  . Поэтому для заданных значений давления
. Поэтому для заданных значений давления  и температуры
и температуры  оно имеет три корня, два из которых могут быть комплексными. Поскольку объём – вещественная величина, то заданным значениям
оно имеет три корня, два из которых могут быть комплексными. Поскольку объём – вещественная величина, то заданным значениям  и
и  соответствуют или три значения объёма
соответствуют или три значения объёма  , или одно.
, или одно.
Для анализа этого уравнения построим изотермы Ван-дер-Ваальса для четырёх различных температур  . (соответственно изотермы . (соответственно изотермы  на рис.5.1). Исследуя графики можно сделать три вывода:
1. При высоких температурах ( на рис.5.1). Исследуя графики можно сделать три вывода:
1. При высоких температурах ( ) изотерма ) изотерма 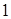 реального газа только некоторым искажением формы отличается от изотермы идеального газа. Изобара реального газа только некоторым искажением формы отличается от изотермы идеального газа. Изобара  , построенная при , построенная при 
|  Рис. 11.1 Изотермы Ван-дер-Ваальса Рис. 11.1 Изотермы Ван-дер-Ваальса
|
(и всякая другая) пересекает её в одной точке  . Следовательно, каждому значению
. Следовательно, каждому значению  при данной температуре
при данной температуре  соответствует единственное значение объёма
соответствует единственное значение объёма  , т.е. уравнение Ван-дер-Ваальса имеет один вещественный корень.
, т.е. уравнение Ван-дер-Ваальса имеет один вещественный корень.
2. На изотермах, полученных при невысоких температурах, ( ) имеются перегибы. Изобара
) имеются перегибы. Изобара  пересекает изотерму
пересекает изотерму  в трёх точках
в трёх точках  . Это соответствует трём вещественным значениям объёма
. Это соответствует трём вещественным значениям объёма  и
и  при давлении
при давлении  и температуре
и температуре  .
.
3. При повышении температуры и переходе от изотермы 4 к изотермам 3 и 2 изгибы на кривых сглаживаются. Расстояние между точками А и С уменьшается, и на изотерме 2 обе точки сливаются в одну – точку перегиба К. Изобара  , проведённая в этой точке, является касательной к изотерме. Температура Т2, соответствующая изотерме с точкой перегиба, называется критической температурой.
, проведённая в этой точке, является касательной к изотерме. Температура Т2, соответствующая изотерме с точкой перегиба, называется критической температурой.
11.4 Критическое состояние вещества. Фазовые переходы
Физическую сущность выводов, полученных при анализе теоретических изотерм Ван-дер-Ваальса, можно выяснить при рассмотрении экспериментальных изотерм.
 Рис. 11.2 Фазовые переходы Рис. 11.2 Фазовые переходы
| На рис. 11.2 приведены экспериментальная (красная) и теоретическая (синяя) изотермы. На участках 1-2 и 3-4 кривые совпадают. На участке 2-3 наблюдается различие. Эксперимент показывает, что на этом участке при уменьшении объёма газа его давление не изменяется. Но в это время (уже в точке 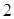 ) на стенках ) на стенках
|
сосуда с газом начинает конденсироваться жидкость. В точке  весь газ превращается в жидкость.
весь газ превращается в жидкость.
Следовательно, в условиях, соответствующих участку изотермы 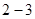 , наблюдается два агрегатных состояния вещества – газообразное и жидкое. Газ в этом случае называется насыщенным паром, а его давление – давлением насыщения
, наблюдается два агрегатных состояния вещества – газообразное и жидкое. Газ в этом случае называется насыщенным паром, а его давление – давлением насыщения  . Если на этом участке приостановить изменение объёма, то процессы испарения и конденсации будут динамически уравновешены. При сжатии жидкости (участок
. Если на этом участке приостановить изменение объёма, то процессы испарения и конденсации будут динамически уравновешены. При сжатии жидкости (участок  ) незначительное уменьшение её объёма приводит к большому увеличению давления, т.к. жидкость практически несжимаема. Состояния, соответствующие участкам
) незначительное уменьшение её объёма приводит к большому увеличению давления, т.к. жидкость практически несжимаема. Состояния, соответствующие участкам  и
и  теоретической изотермы, при некоторых условиях практически осуществимы, но неустойчивы (метастабильны). Участок
теоретической изотермы, при некоторых условиях практически осуществимы, но неустойчивы (метастабильны). Участок  соответствует пару, находящемуся под давлением, большим, чем давление насыщенного пара при той же температуре. Он называется пересыщенным паром. Участок
соответствует пару, находящемуся под давлением, большим, чем давление насыщенного пара при той же температуре. Он называется пересыщенным паром. Участок  соответствует жидкости, находящейся под давлением, меньшим давления насыщенного пара при данной температуре Т. Это перегретая жидкость.
соответствует жидкости, находящейся под давлением, меньшим давления насыщенного пара при данной температуре Т. Это перегретая жидкость.
Если при различных температурах получить серию экспериментальных изотерм и соединить крайние точки их горизонтальных участков, то получится
 Рис. 11.3 Серия изотерм Ван-дер-Ваальса Рис. 11.3 Серия изотерм Ван-дер-Ваальса
| колоколообразная кривая. Эта кривая и участок критической изотермы, лежащей слева от точки перегиба  , делят ( , делят (  ) диаграмму на три области: область двухфазных состояний (под колоколообразной кривой), область жидкого состояния (слева) и область пара (справа). Выше критической изотермы находится газ, который никаким сжатием не может быть превращён в жидкость. ) диаграмму на три области: область двухфазных состояний (под колоколообразной кривой), область жидкого состояния (слева) и область пара (справа). Выше критической изотермы находится газ, который никаким сжатием не может быть превращён в жидкость.
|
Объём  и давление
и давление  , соответствующие точке
, соответствующие точке  , называются критическими. Состояние с критическими параметрами:
, называются критическими. Состояние с критическими параметрами:
 , (11.5)
, (11.5)
называется критическим (где а и b – поправки Ван-дер-Ваальса,  – молярная газовая постоянная). Таким образом, уравнение Ван-дер-Ваальса описывает газообразное состояние вещества, процесс перехода газа в жидкость и сжатие жидкости.
– молярная газовая постоянная). Таким образом, уравнение Ван-дер-Ваальса описывает газообразное состояние вещества, процесс перехода газа в жидкость и сжатие жидкости.
11.5 Внутренняя энергия реального газа
Внутренняя энергия идеального газа целиком определяется кинетической энергией теплового движения молекул и зависит только от его температуры:

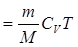 , (11.6)
, (11.6)
где  – молярная теплоёмкость газа при постоянном объёме,
– молярная теплоёмкость газа при постоянном объёме,  – число степеней свободы молекул газа. При вычислении внутренней энергии реальных газов необходимо также учитывать потенциальную энергию
– число степеней свободы молекул газа. При вычислении внутренней энергии реальных газов необходимо также учитывать потенциальную энергию  , обусловленную силами межмолекулярного взаимодействия
, обусловленную силами межмолекулярного взаимодействия
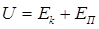 . (11.7)
. (11.7)
Силы молекулярного сцепления вызывают появление дополнительного внутреннего давления (11.2)
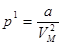 ,
,
их работа приводит к изменению потенциальной энергии
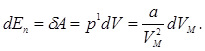
Проинтегрируем полученное выражение:
 .
.
При безграничном увеличении объёма расстояния между молекулами возрастают и потенциальную энергию следует принять равной нулю, поэтому и постоянная интегрирования  принимает нулевое значение (
принимает нулевое значение ( ). Складывая кинетическую и потенциальную энергии, получим, что, внутренняя энергия реального газа зависит от его температуры
). Складывая кинетическую и потенциальную энергии, получим, что, внутренняя энергия реального газа зависит от его температуры  и объёма
и объёма  :
:
 . (11.8)
. (11.8)
Из первого закона термодинамики ( ) следует, что при адиабатном расширении газа (
) следует, что при адиабатном расширении газа ( ) без совершения работы (
) без совершения работы ( ) (расширение газа в вакуум) внутренняя энергия газа не изменяется (
) (расширение газа в вакуум) внутренняя энергия газа не изменяется ( и
и  ).
).
Это равенство формально справедливо как для идеального, так и для реального газов, но его физический смысл для обоих случаев различен.
Для идеального газа равенство  означает равенство температур (
означает равенство температур ( ), т.е. при адиабатном расширении идеального газа в вакуум его температура не изменяется.
), т.е. при адиабатном расширении идеального газа в вакуум его температура не изменяется.
Из (11.8) следует, что внутренняя энергия реального газа не изменится, если адиабатное изменение его объёма будет сопровождаться изменением температуры газа, причём  и
и  будут иметь разные знаки.Следовательно, при адиабатном расширенииреального газа в вакуум он охлаждается, а при адиабатном сжатии в вакуум – нагревается
будут иметь разные знаки.Следовательно, при адиабатном расширенииреального газа в вакуум он охлаждается, а при адиабатном сжатии в вакуум – нагревается
Не нашли, что искали? Воспользуйтесь поиском: