Изопроцессы, Адиабатический, политропный

Изопроцессы

Для равновесных процессов изменения состояния газа первое начало термодинамики можно записать в виде

. (6.4)

Примение этого уравнения совместно с уравнением (5.5) Менделеева-Клапейрона позволяет получить законы и уравнения изопроцессов для идеального газа.

Адиабатный процесс (). Практически адиабатными можно считать процессы быстрого расширения или сжатия газа, при которыхсистема не обменивается теплотой с окружающей средой.Из первого начала термодинамики (6.1) для адиабатного процесса () получаем, что система совершает работу за счёт убыли её внутренней энергии:

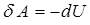. (6.15)

Подставим сюда выражения (6.2) и (6.6) получим, что работа, связанная с изменением объёма газа, сопровождается изменением его температуры:

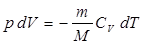(6.16)

Знак «минус» в уравнении означает, что увеличение объёма (расширение) сопровождается понижением температуры, а уменьшение объёма (сжатие) – повышением. Уравнение адиабаты или уравнение Пуассона имеет вид:

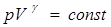, (6.17)

где – безразмерная величина, называемаяпоказателем адиабаты или коэффициентом Пуассона. Уравнение адиабаты можно записать и через другие параметры состояния:

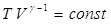и 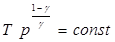. (6.18)

На графике (рис. 6.1) (так как ), адиабата идёт круче изотермы. Объясняется это тем, что при адиабатном сжатии увеличение давления происходит не только за счёт уменьшения объёма, как при изотермическом сжатии, но и за счёт увеличения температуры сжимаемого газа. При адиабатном расширении газа его температура уменьшается, и давление падает быстрее, чем при соответствующем изотермическом расширении. Работа, совершаемая газом в адиабатном процессе:

, (6.19)

Политропный процесс (). Политропный процесс – термодинамический процесс, протекающий без изменения теплоёмкости . Уравнение политропы имеет вид:

, (6.20)

где – показатель политропы ( – теплоёмкость газа в данном процессе). Все рассмотренные выше изопараметрические процессы являются частными случаями политропного процесса.

Рис.6.1 Политропный процесс

В этом можно убедиться, если

уравнение , преобразовать к виду 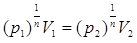. При 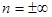получаем . Все эти процессы

изображены на приведённой диаграмме (рис.6.1).

Не нашли, что искали? Воспользуйтесь поиском: