Диффузией называется самопроизвольное выравнивание концентрации смеси различных веществ, происходящее вследствие теплового движения частиц вещества.

9.1.Основные понятия и определения

Теория теплопередачи, или теплообмена, представляет собой учение о процессах распространения теплоты в пространстве с неоднородным полем температур.

Существуют три основных вида теплообмена: теплопроводность, конвекция и тепловое излучение.

Теплопроводность — это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов).

Конвекция осуществляется путем перемещения в пространстве не­равномерно нагретых объемов среды. При этом перенос теплоты не­разрывно связан с переносом самой среды.

Тепловое излучение характеризуется переносом энергии от одного тела к другому электромагнитными волнами.

Часто все способы переноса теплоты осуществляются совместно. Например, конвекция всегда сопровождается теплопроводностью, так как при этом неизбежно соприкосновение частиц, имеющих различные температуры.

Совместный процесс переноса теплоты конвекцией и теплопроводностью называется конвективным теплообменом. Частным случаем конвективного теплообмена является теплоотдача — конвективный теплообмен между твердой стенкой и движущейся средой. Теплоотдача может сопровождаться тепловым излучением. В этом случае перенос теплоты осуществляется одновременно теплопроводностью, конвекцией и тепловым излучением.

Многие процессы переноса теплоты сопровождаются переносом вещества — массообменном, который проявляется в установлении равновесной концентрации вещества.

Совместное протекание процессов теплообмена и массообменна называется тепломассообменном.

Теплопроводность определяется тепловым движением микрочастиц тела. В чистом виде явление теплопроводности наблюдается в твердых телах, неподвижных газах и жидкостях при условии невозможности возникновения в них конвективных токов.

Передача теплоты теплопроводностью связана с наличием разности температур тела. Совокупность значений температур всех точек тела в данный момент времени называется температурным полем. В общем случае уравнение температурного поля имеет вид:

,

(9.1)

где t — температура тела; х, у, z — координаты точки; τ — время. Такое температурное поле называется нестационарным и отвечает неустановившемуся режиму теплопроводности. Если температура тела не изменяется с течением времени, то температурное поле называется стационарным. Тогда

, .

(9.2)

Температура может быть функцией одной, двух и трех координат, соответственно температурное поле будет одно-, дву- и трехмерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля:

; ; .

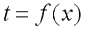Если соединить все точки тела с одинаковой температурой, то получим поверхность равных температур, называемую изотермической. Так как в определенной точке тела в данный момент времени может быть только одна температура, изотермические поверхности не пересекаются; все они либо замыкаются на себя, либо заканчиваются на границе тела. Пересечение изотермных поверхностей плоскостью дает на ней семейство изотерм. Интенсивность изменения температуры в каком-либо направлении характеризуется производной 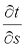, принимающей наибольшее значение в направлении нормали к изотермической поверхности

.

(9.3)

Вектор называется температурным градиентом и является мерой интенсивности изменения температуры в направлении по нормали к изотермной поверхности. Направлен он в сторону возрастания температуры.

9.2.Закон Фурье

Согласно гипотезе Фурье, количество теплоты d²Q_τ, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту :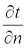

.

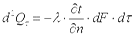(9.4)

Здесь множитель λ называется коэффициентом теплопроводности. Знак минус указывает на то, что теплота передается в направлении уменьшения температуры. Количество теплоты, прошедшее в единицу времени через единицу изотермической поверхности, называется плотностью теплового потока:

.

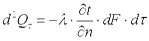(9.5)

Проекции вектора q на координатные оси соответственно:

; ; .

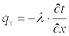Уравнения (9.4) и (9.5) являются математическим выражением основного закона теплопроводности — закона Фурье.

Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком:

.

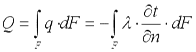(9.6)

Полное количество теплоты, прошедшее через эту поверхность за время τ, определится из уравнения

 

.

(9.7)

29. ТЕПЛОЁМКОСТЬ ГАЗОВ

 

2.1.Массовая, объёмная и мольная удельные теплоёмкости

Известно, что подвод теплоты к рабочему телу или отвод теплоты от него в каком-либо процессе приводит к изменению его температуры. Отношение количества тепло­ты, подведенной (или отведенной) в данном процессе, к изменению температуры называется теплоемкостью тела (системы тел):

,

(2.1)

где — элементарное количество теплоты; — элементарное изменение температуры.

Теплоемкость численно равна количеству теплоты, которое необходимо подвести к системе, чтобы при заданных условиях повысить ее температуру на 1 градус. Так как единицей количества теплоты в СИ является джоуль, а температуры — градус К, то единицей теплоемкости будет Дж/К.

В зависимости от внешних условий и характера термодинамического процесса теплота 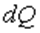может либо подводиться к рабочему телу, либо отводиться от него. Учитывая, что система участвует в бесчисленном множестве процессов, сопровождающихся теплообменом, величина 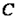для одного и того же тела может иметь различные значения. В общем случае значение теплоёмкости 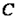лежит в интервале от -∞ до +∞, то есть она может быть любой положительной или отрицательной величиной.

Поэтому обычно в выражении (2.1) при теплоёмкости 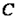указывается индекс "x", который характеризует вид процесса теплообмена

.

(2.2)

Индекс "x" означает, что процесс подвода (или отвода) теплоты идет при постоянном значении какого-либо из параметров, например, давления 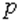, объема или других.

Ввиду того, что в термодинамике обычно рассматриваются квазистатические процессы теплообмена, теплоемкость 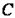является величиной, относящейся к системе, которая находится в состоянии термодинамического равновесия. Таким образом, теплоемкости являются функциями параметров термодинамической системы. Для простых систем — это функции каких-либо двух из трех параметров: , , .

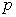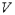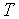Опыты показывают, что количество теплоты, подведенное к рабочему телу системы или отведенное от него, всегда пропорционально количеству рабочего тела. Для возможности сравне­ния вводят, как известно, удельные величины теплоемкости, относя подведенную (или отведенную) теплоту количественно к единице рабочего тела.

В зависимости от количественной единицы тела, к которому подводится теплота в термодинамике, различают массовую, объемную и мольную теплоемкости.

Массовая теплоемкость — это теплоемкость, отнесенная к единице массы рабочего тела,

.

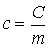Единицей измерения массовой теплоемкости является Дж/(кг • К). Массовую теплоемкость называют также удельной теплоемкостью.

Объемная теплоемкость — теплоемкость, отнесенная к единице объема рабочего тела,

,

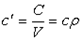где и 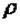— объем и плотность тела при нормальных физических условиях.

Объемная теплоемкость измеряется в Дж/(м3 • К).

Мольная теплоемкость — теплоемкость, отнесенная к количеству рабочего тела (газа) в молях,

,

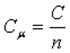(2.3)

где — количество газа в молях.

Мольную теплоемкость измеряют в Дж/(моль • К).

Массовая и мольная теплоемкости связаны следующим соотношением:

или

,

(2.4)

где 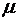- молекулярная масса.

Объемная теплоемкость газов выражается через мольную как

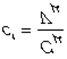
или

,

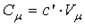(2.5)

где 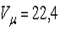м3/моль — мольный объем газа при нормальных условиях.

 

2.2.Средняя и истинная теплоёмкости

Учитывая, что теплоемкость непостоянна, а зависит от температуры и других термических параметров, различают истинную и среднюю теплоемкости. Истинная теплоемкость выражается уравнением (2.2) при определенных параметрах термодинамического процесса, то есть в данном состоянии рабочего тела. В частности, если хотят подчеркнуть зависимость теплоёмкости рабочего тела от температуры, то записывают её как 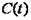, а удельную – как 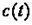. Обычно под истинной теплоёмкостью понимают отношение элементарного количества теплоты, которое сообщается термодинамической системе в каком-либо процессе к бесконечно малому приращению температуры этой системы, вызванному сообщенной теплотой. Будем считать истинной теплоёмкостью термодинамической системы при температуре системы равной 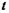, а 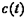- истинной удельной теплоёмкостью рабочего тела при его температуре равной . Тогда среднюю удельную теплоёмкость рабочего тела при изменении его температуры от до 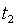можно определить как

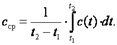
(2.6)

Обычно в таблицах приводятся средние значения теплоемкости 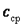для различных интервалов температур, начинающихся с 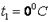. Поэтому во всех случаях, когда термодинамический процесс проходит в интервале температур от 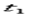до 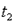, в котором 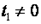, количество удельной теплоты 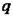процесса определяется с использованием табличных значений средних теплоемкостей следующим образом:

.

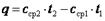(2.7)

Значения средних теплоемкосте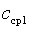й и 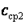, находят по таблицам.

 

2.3.Теплоёмкости при постоянном объёме и давлении

Особый интерес представляют средние и истинные теплоемкости в процессах при постоянном объеме (изохорная теплоемкость, равная отношению удельного количества теплоты в изохорном процессе к изменению температуры рабочего тела dT) и при постоянном давлении 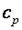(изобарная теплоемкость, равная отношению удельного количества теплоты в изобарном процессе к изменению температуры рабочего тела dT).

Для идеальных газов связь между изобарной и изохорной теплоёмкостями и устанавливается известным уравнением Майера .

Из уравнения Майера следует, что изобарная теплоемкость больше изохорной на значение удельной характеристической постоянной идеального газа. Это объясняется тем, что в изохорном процессе () внешняя работа не выполняется и теплота расходуется только на изменение внутренней энергии рабочего тела, тогда как в изобарном процессе () теплота расходуется не только на изменение внутренней энергии рабочего тела, зависящей от его температуры, но и на совершение им внешней работы.

Для реальных газов 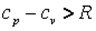, так как при их расширении и 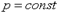совершается работа не только против внешних сил, но и внутренняя работа против сил взаимодействия между молекулами газа, на что дополнительно расходуется теплота.

В

 

теплотехнике широко применяется отношение теплоемкостей 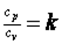, которое носит название коэффициента Пуассона (показателя адиабаты). В табл. 2.1 приведены значения 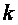некоторых газов, полученные экспериментально при температуре 15 °С.

Таблица 2.1
Газ	Показатель адиабаты
Гелий	1,660
Аргон	1,667
Окись углерода	1,401
Кислород	1,398
Водород	1,408
Азот	1,41
Водяной пар	1,33
Углекислый газ	1,305
Аммиак	1,313
Метан	1,315

Теплоемкост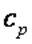и и 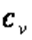зависят от температуры, следовательно, и показатель адиабаты 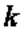должен зависеть от температуры.

Известно, что с повышением температуры теплоёмкость 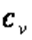увеличивается. Поэтому с ростом температуры 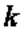уменьшается, приближаясь к единице. Однако всегда остается больше единицы. Обычно зависимость показателя адиабаты от температуры выражается формулой вида

,

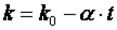где 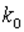- значение коэффициента при 0⁰ С; 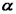- коэффициент, принимающий для каждого газа своё постоянное значение.

Кроме того, можно установить следующие широко использующиеся зависимости.

,

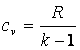(2.8)

и так как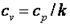

.

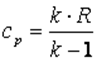(2.9)

⇐ Предыдущая567891011121314Следующая ⇒

---

Не нашли, что искали? Воспользуйтесь поиском: