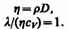ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вывод основного уравнения МКТ
Частицы идеального газа при соударениях с границами емкости ведут себя как упругие тела. Такое взаимодействие описывается согласно законам механики. При соприкосновении частицы с границей емкости проекция vx скоростного вектора на ось ОХ, проходящую под прямым углом к границе сосуда, меняет свой знак на противоположный, но сохраняется неизменной по модулю:
Поэтому после соударения частицы с границей емкости проекция импульса молекулы на ось ОХ меняется с mv1x = –mvx на mv2x = mvx.
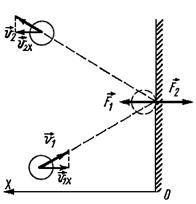
Изменение импульса молекулы ΔP равняется удвоенному произведению массы молекулы на ее скорость:
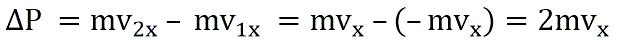
Поскольку в каждом из шести основных направлений декартовой системы координат (вверх, вниз, вперед, назад, вправо, влево) движется одна шестая часть частиц N/6. Тогда число частиц, которые сталкиваются с каждой стенкой за время Δt равно:
S – площадь этой стенки
n - концентрация частиц
Давление p равно отношению силы F к площади S, на которую действует эта сила:
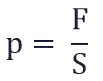
Суммарная сила, с которой частицы давят на стенку равна отношению произведения числа этих частиц N и изменения импульса ΔP ко времени, в течение которого происходит давление:
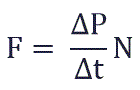
Исходя из вышенаписанного получаем:
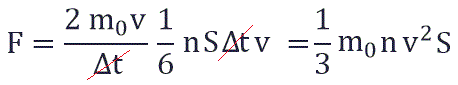
Тогда
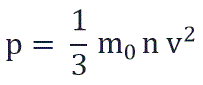
Если заменить среднее значение кинетической энергии поступательного движения молекул - E:
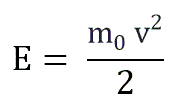
и подставить эту формулу в основное уравнение МКТ, получим давление идеального газа:
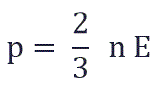
Давление идеального газа равняется двум третям средней кинетической энергии поступательного движения молекул на единицу объема. При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.
Из (8.32) получим выражения для среднего значения модуля скорости u и среднего значения квадрата u:
 , (8.33)
, (8.33)
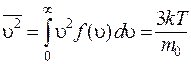 . (8.34)
. (8.34)
Таким образом, средняя скорость молекул (ее называют также средней арифметической скоростью) имеет значение
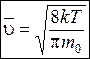 . (8.35)
. (8.35)
Квадратный корень из выражения (8.34) дает среднюю квадратичную скорость молекул:
 . (8.36)
. (8.36)
Отметим, что она совпадает с формулой (8.24). На рис. 8.5 приведен график функции распределения Максвелла. Вертикальными линиями отмечены три характерные скорости  .
.
25.Звкон Максвелла о распределении молекул газа по скоростям.
Движение молекул газа подчиняется законам статистической физики. В среднем скорости и энергии всех молекул одинаковы. Однако в каждый момент времени энергия и скорости отдельных молекул могут значительно отличаться от среднего значения.
С помощью теории вероятности Максвеллу удалось вывести формулу для относительной частоты, с которой в газе при данной температуре встречаются молекулы со скоростями в определенном интервале значений.
Закон распределения Максвелла определяет относительное число молекул dN/N, скорости которых лежат в интервале (u, u + du). Оно имеет вид:
 (8.29)
(8.29)
где N – общее число молекул газа; 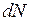 – число молекул, скорости которых заключены в определенном интервале; u – нижняя граница интервала скоростей; d u – величина интервала скоростей; T – температура газа; e = 2,718… – основание натуральных логарифмов;
– число молекул, скорости которых заключены в определенном интервале; u – нижняя граница интервала скоростей; d u – величина интервала скоростей; T – температура газа; e = 2,718… – основание натуральных логарифмов;
k = 1,38×10-23 Дж/К – постоянная Больцмана; m 0 – масса молекулы.
При получении этой формулы Максвелл основывался на следующих предположениях:
1. Газ состоит из большого числа N одинаковых молекул.
2. Температура газа постоянна.
3. Молекулы газа совершают тепловое хаотическое движение.
4. На газ не действуют силовые поля.
Отметим, что под знаком экспоненты в формуле (8.29) стоит отношение кинетической энергии молекулы  к величине kT, характеризующей среднее (по молекулам) значение этой энергии.
к величине kT, характеризующей среднее (по молекулам) значение этой энергии.
Распределение Максвелла показывает, какая доля dN/N общего числа молекул данного газа обладает скоростью в интервале от u до u + du.
График функций распределения (рис. 8.5) асимметричен. Положение максимума характеризует наиболее часто встречающуюся скорость, которую называют наиболее вероятной скоростью um. Скорости, превышающие um, встречаются чаще, чем меньшие скорости. С повышением температуры максимум распределения сдвигается в направлении больших скоростей.
Одновременно кривая становится более плоской (площадь, заключенная под кривой, не может измениться, так как число молекул N остается постоянным).
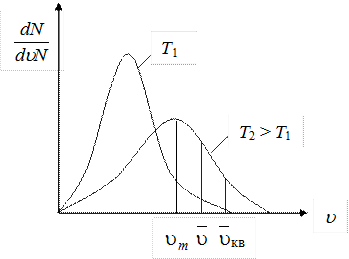
Рис. 8.5
Для определения наиболее вероятной скорости нужно исследовать на максимум функцию распределения Максвелла (приравнять первую производную к нулю и решить относительно u). В результате получаем
 .
.
Мы опустили множители, не зависящие от u. Осуществив дифференцирование, придем к уравнению
 .
.
Первый сомножитель (экспонента) обращается в нуль при u = ¥, а третий сомножитель (u) при u = 0. Однако из графика (рис. 8.5) видно, что значения u = 0 и u = ¥ соответствуют минимумам функции (8.29). Следовательно, значение u, отвечающее максимуму, получается из равенства нулю второй скобки:  . Отсюда
. Отсюда
 . (8.30)
. (8.30)
Введем обозначения для функции распределения молекул по скоростям (8.29):
 . (8.31)
. (8.31)
Известно, что среднее значение некоторой физической величины j(x) можно вычислить по формуле
 . (8.32)
. (8.32)
| 26.Барометрическая формула | ||||||
В данном разделе мы выведем зависимость давления газа P от высоты h над уровнем моря в гравитационном поле Земли. Возьмем произвольную цилиндрическую колонну газа с площадью сечения S и высотой h. Вес выделенного объема газа будет равен
F=mg=ρgV=ρghS,
где ρ означает плотность газа. Плотность газа будет выражаться следующей формулой:
P=FS=ρghSS=ρgh.
Теперь представим такую колонну в атмосфере и выделим в ней тонкий слой воздуха высотой dh (рисунок 1). Ясно, что такой слой вызывает изменение давления на величину
dP=−ρgdh.
Мы поставили здесь знак минус, поскольку давление должно уменьшаться с увеличением высоты.
Рассматривая атмосферный воздух как идеальный газ, воспользуемся уравнением Менделеева-Клапейрона, чтобы выразить плотность ρ через давление P: PV=mMRT,⇒P=mVMRT=ρMRT. Здесь T − абсолютная температура, R − универсальная газовая постояная, равная 8.314ДжK⋅моль, M − молярная масса, которая для воздуха равна 0.029кгмоль. Отсюда следует, что плотность определяется формулой ρ=MPRT. Подставляя это в дифференциальное соотношение для dP, находим: dP=−ρgdh=−MPRTgdh,⇒dPP=−MgRTdh. В результате мы получаем дифференциальное уравнение, описывающее давление газа P как функцию высоты h. Интегрирование приводит к следующему уравнению: ∫dPP=−∫MgRTdh,⇒lnP=−MgRTh+lnC. Избавляясь от логарифмов, получаем так называемую барометрическую формулу P=Cexp(−MgRTh). Константа C определяется из начального условия P(h=0)=P0, где P0 − это среднее атмосферное давление над уровнем моря. P=P0exp(−MgRTh). Подставляя известные стандартные значения (смотрите рисунок 2 выше), находим зависимость P(h)(в килопаскалях), которая описывается формулой P(h)=101.325exp(−0.02896⋅9.8078.3143⋅288.15h)=101.325exp(−0.00012h)[кПа], где высота h над уровнем моря выражается в метрах. P(h)=760exp(−0.00012h)[мм.рт.ст.]. Барометрическая формула широко используется для оценки атмосферного давления при различных условиях, хотя она дает слегка завышенные значения.
Явления переноса в термодинамически неравновесных системах В термодинамически неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы, импульса. К явлениям переноса относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса). Для простоты ограничимся одномерными явлениями переноса. Систему отсчета выберем так, чтобы ось х была ориентирована в направлении переноса. 1. Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше,чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур. Перенос энергии в форме теплоты подчиняется закону Фурье:
где jE — плотность теплового потока — величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х, l — теплопроводность, Можно показать, что
где сV — удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме), r— плотность газа, < v > — средняя скорость теплового движения молекул, < l > — средняя длина свободного пробега. 2. Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Во время становления молекулярно-кинетической теории по вопросу диффузии возникли противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространяется довольно медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь с другими молекулами, в основном «стоят» на месте. Явление диффузии для химически однородного газа подчиняется закону Фука:
где jm — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, D — диффузия (коэффициент диффузии), d r/ d x — градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности (поэтому знаки jm иd r/ d x противоположны). Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице. Согласно кинетической теории газов,
3. Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Согласно формуле (31.1), сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:
где h — динамическая вязкость (вязкость), d v/ d x — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев, S — площадь, на которую действует сила F. Взаимодействие двух слоев согласно второму закону Ньютона можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе. Тогда выражение (48.5) можно представить в виде
где jp — плотность потока импульса — величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х, Динамическая вязкость h численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле
Из сопоставления формул (48.1), (48.3) и (48.6), описывающих явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Эти законы были установлены задолго до того, как они были обоснованы и выведены из молекулярно-кинетической теории, позволившей установить, что внешнее сходство их математических выражений обусловлено общностью лежащего в основе явлений теплопроводности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения и столкновений друг с другом. Рассмотренные законы Фурье, Фика и Ньютона не вскрывают молекулярно-кинетического смысла коэффициентов l, D и h. Выражения для коэффициентов переноса выводятся из кинетической теории. Они записаны без вывода, так как строгое рассмотрение явлений переноса довольно громоздко, а качественное — не имеет смысла. Формулы (48.2), (48.4) и (48.7) связывают коэффициенты переноса и характеристики теплового движения молекул. Из этих формул вытекают простые зависимости между l, D и h:
Используя эти формулы, можно по найденным из опыта одним величинам определить другие. |
Не нашли, что искали? Воспользуйтесь поиском:


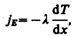 (48.1)
(48.1) — градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки jE и
— градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки jE и 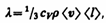 (48.2)
(48.2)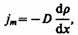 (48.3)
(48.3)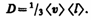 (48.4)
(48.4)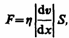 (48.5)
(48.5) (48.6)
(48.6) — градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки jр и
— градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки jр и 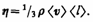 (48.7)
(48.7)