ПОПЕРЕЧНЫЕ И ПРОДОЛЬНЫЕ ВОЛНЫ. УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ.

Различают поперечные и продольные волны. В поперечной волне частицы среды колеблются перпендикулярно направлению её распространения, в продольной волне – вдоль него. На рис.7.7 представлен процесс образования поперечной волны, распространяющейся вдоль оси . На каждой строчке показано положение нескольких частиц в выбранный момент времени. Частицы волны движутся вверх и вниз около равновесного положения. Волна не «бежит» в направлении распространения, происходит только передача колебательного движения и его энергии. Основным свойством всех бегущих волн является перенос энергии без переноса вещества.

Длиной волны 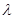называется расстояние между ближайшими частицами, колеблющимися в одинаковой фазе. Это расстоянию, на которое распространяется волна за время, равное периоду колебаний : , (7.21) где – скорость распространения волны; – частота колебаний. При распространении волнового процесса колеблется вся совокупность частиц, заключенных в некотором объёме.

Рис.7.7 Поперечная волна

Геометрическое место точек, до которых доходят колебания к моменту времени , называется фронтом волны (волновым фронтом). Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновые поверхности могут иметь любую форму. В простейших случаях это плоскость или сфера. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической волне – множество концентрических сфер.

4.5.6 Уравнение плоской бегущей волны

Уравнение волны описывает зависимость смещения колеблющейся частицы от координат и времени :

. (7.22)

Рис.7.8

Пусть точки, расположенные в плоскости , совершают колебания по закону . В точке (рис.7.8), расположенной на расстоянии от источника , колебания частиц среды будут происходить по тому же закону, но с отставанием по времени на (где - скорость распространения волны):

. (7.23)

Так как точка была выбрана произвольно, то уравнение (7.23) позволяет определить смещение любой точки среды, вовлечённой в колебательный процесс, в любой момент времени, поэтому называется уравнением плоской бегущей волны. В общем случае оно имеет вид:

(7.24)

где - амплитуда волны; – фаза плоской волны; – циклическая частота волны; – начальная фаза колебаний. Подставляя в это уравнение выражения для скорости () и циклической частоты (), получим:

(7.25)

Если ввести волновое число , то уравнение плоской волны можно записать в виде:

. (7.26)

ВОПРОС №22

Не нашли, что искали? Воспользуйтесь поиском: