ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Центр масс механической системы и закон его движения
Центром масс (или центром инерции) системы материальных точек называется воображаемая точка 
, радиус-вектор которой равен
, (2.7)
где 
и 
– масса и радиус-вектор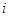 
-й материальной точки; 
– суммарная масса системы; 
– общее число точек в системе. Скорость движения точки определяется
(2.8)
Следовательно, импульс системы
(2.9)
Подставив это выражение в основной закон динамики (2.5), получим
(2.10)
что центр масс механической системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная главному вектору внешних сил, приложенных к системе.
Из закона следует, что скорость 
движения центра масс замкнутой механической системы не изменяется с течением времени, он либо покоится, либо движется прямолинейно и равномерно.
9) Момент силы - осевой вектор, его направление определяется правилом правого винта. Соотношение (2.10), определяющее численное значение момента силы 
, можно записать в векторной форме
. (2.11)
Произведение массы материальной точки на квадрат ее расстояния от оси вращения 
называют моментом инерции материальной точки относительно этой оси и обозначают через 
(2.12)
Момент импульса и закон его сохранения.
Моментом импульса (количества движения) материальной точки A относительно неподвижной точки O называется физическая величина,
определяемая векторным произведением
L =[ r, p ]=[ r, m υ].
Моментом импульса относительно неподвижной оси z называется скалярная
величина Lz, равная проекции на эту ось
вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса Lz не зависит от положения точки O на оси z
При вращении абсолютно твердого тела
вокруг неподвижной оси каждая точка тела движется по окружности постоянного радиуса ri со скоростью υi перпендикулярной радиусу. Момент импульса
отдельной частицы равен Liz = mi υ iri и направлен по оси в сторону, определяемую правилом правого винта (совпадает с направлением вектора угловой скоростиω).
10) Момент инерции тела – величина, определяющая его инертность во вращательном движении.
Суммируя вращающие моменты (2.10), приложенные ко всем элементам масс, составляющих тело, получим:
, (2.13)
где 
суммарный момент сил, приложенных к телу.
Момент инерции тела относительно оси вращения равен сумме моментов инерции всех его материальных точек относительно этой оси:
(2.14)
Не нашли, что искали? Воспользуйтесь поиском: