Закон Ампера. Взаимодействие параллельных токов.

Ампер установил, что сила d F, с которой магнитное поле действует на элемент проводника d l с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины d l проводника на магнитную индукцию В:

d F = I[d l, B ] (3.1)

Направление вектора d F может быть найдено по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входили линии магнитной индукции, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера (3.1) вычисляется по формуле

dF = I B dl s inα, (3.2)

где α – угол между векторами dl и В.

Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I ₁, и I ₂ (направления токов указаны на рис. 8), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I ₁, на элемент d l второго проводника с током I ₂. Ток I ₁ создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора В ₁, задается правилом правого винта, его модуль по формуле (2.6) равен

.

Направление силы d F ₂, с которой поле В ₁, действует на участок d l второго тока определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (3.2), с учетом того, что угол α между элементами тока I ₂, и вектором В ₁ прямой, равен dF ₂= I ₂ B ₁ dl, или, подставляя значение для В ₁, получим

. (3.3)

Рассуждая аналогично, можно показать, что сила d F ₁, с которой магнитное поле тока I ₂ действует на элемент d l первого проводника с током I ₁, направлена в противоположную сторону и по модулю равна

. (3.4)

Сравнение выражений (3.3) и (3.4) показывает, что dF ₁= dF ₂,т.е. два параллельных тока одинакового направления притягиваются друг к другу с силой

. (3.5)

Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (3.5).

54)Работа по перемещению проводника с током в магнитном поле На проводник с током в магнитном поле действуют силы, определяемые законом Ампера. Если проводник не закреплен, то под действием силы Ампера он будет в магнитном поле перемещаться – магнитное поле совершает работу по перемещению проводника с током.

Элементарная работа , совершаемая силой Ампера 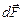при малом перемещении в постоянном магнитном поле малого элемента проводника с током , равна , где вектор малой площадки, прочерчиваемый элементом проводника при его малом перемещении (см. рис.), а магнитный поток сквозь эту площадку.

Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником: , где поток вектора магнитной индукции, пронизывающий площадь, пересекаемую проводником в магнитном поле.

При малом перемещении в магнитном поле проводника конечной длины магнитный поток сквозь поверхность, которую прочерчивает весь проводник при его малом перемещении .

Если сила тока постоянна и проводник совершил перемещение из положения 1 в положение 2, то работа сил Ампера .

Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока на изменение магнитного потока: , где изменение магнитного потока, сцепленного с контуром или магнитный поток через поверхность, прочерченную контуром. Формула справедлива для контура любой формы в произвольном магнитном поле.

Замечание. Когда в задаче рассматривается замкнутый контур, находящийся в магнитном поле, то различают два случая:

1) магнитное поле однородно. Тогда на контур с током действует вращающий момент, определяемый формулой . Под влиянием этого момента контур поворачивается так, что угол между векторами и уменьшается. При наступает состояние устойчивого равновесия контура в магнитном поле;

2) магнитное поле неоднородно. В этом случае на контур с током кроме вращающего момента действует сила, определяемая формулой 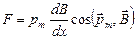, где направление быстрейшего изменения величины . Эта формула справедлива, если:

· магнитное поле таково, что направления оси 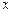и вектора совпадают (напр., поле соленоида в точках, лежащих на его оси вблизи концов соленоида);

· контур с током достаточно мал для того, чтобы во всех точках ограниченной им плоскости можно было считать величину приблизительно одинаковой.

Не нашли, что искали? Воспользуйтесь поиском: