ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Сила Лоренца, движение заряженных частиц в магнитном поле.
| |
|
где dl — вектор элементарной длины контура, который направлен вдоль обхода контура, B l =Bcosα — составляющая вектора В в направлении касательной к контуру (с учетом выбора направления обхода контура), α — угол между векторами В и dl. Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной μ0 на алгебраическую сумму токов, охватываемых этим контуром: 
(1) где n — число проводников с токами, которые охватываются контуром L любой формы. Каждый ток в уравнении (1) учитывается столько раз, сколько раз он охватывается контуром. Ток считается положительным, если его направление образует с направлением обхода по контуру правовинтовую систему; отрицательным считается ток противоположного направления.
Рис.1 Например, для системы токов, изображенных на рис. 1, 
Выражение (1) выполняется только для поля в вакууме, поскольку, как будет показано дальше, для поля в веществе нужно учитывать молекулярные токи.
Рис.2
Продемонстрируем справедливость теоремы о циркуляции вектора В на примере магнитного поля прямого тока I, который перпендикулярн плоскости чертежа и направлен к нам (рис. 2). Возьмем в качестве контура окружность радиуса r. В каждой точке этого контура вектор Водинаков по модулю и направлен по касательной к окружности (она есть и линия магнитной индукции). Значит, циркуляция вектора В равна 
Используя формулу (1), получим В•2πr=μ0I (в вакууме), откуда 
Значит, используя теорему о циркуляции вектора В мы получили выражение для магнитной индукции поля прямого тока, выведенное ранее на основании закона Био-Савара-Лапласа. Сравнивая выражения для циркуляции векторов Е и В, можно увидеть, что между ними существует принципиальное различие. Циркуляция вектора Е электростатического поля всегда равна нулю, т. е. электростатическое поле потенциально. Циркуляция вектора В магнитного поля не равна нулю. Такое поле носит название вихревое. Теорема о циркуляции вектора В имеет в теории о магнитном поле такое же значение, как теорема Гаусса в электростатике, поскольку дает возможность находить магнитную индукцию поля без использования закона Био-Савара-Лапласа.
| 57) Магнитный поток Теорема Гаусса для магнитной индукции | |
Как было показано выше, в природе нет магнитных зарядов. В 1931 г. П. Дирак высказал предположение о существовании обособленных магнитных зарядов, названных впоследствии монополи Дирака. Однако до сих пор они не найдены. Это приводит к тому, что линии вектора
В соответствии с вышеизложенным, можно сделать заключение, что поток вектора Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие:
Это теорема Гаусса для Этот результат является математическим выражением того, что в природе нет магнитных зарядов – источников магнитного поля, на которых начинались и заканчивались бы линии магнитной индукции. Заменив поверхностный интеграл в (1.7.1) объемным, получим:
где Это условие должно выполняться для любого произвольного объема V, а это, в свою очередь, возможно, если подынтегральная функция в каждой точке поля равна нулю. Таким образом, магнитное поле обладает тем свойством, что его дивергенция всюду равна нулю:
В этом его отличие от электростатического поля, которое является потенциальным и может быть выражено скалярным потенциалом φ, магнитное поле – вихревое, или соленоидальное (см. рис. 1.3 и 1.8).
Компьютерная модель магнитного поля Земли, подтверждающая вихревой характер, изображена на рис. 1.9.
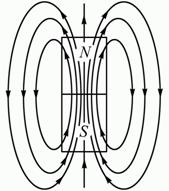
Рис 1.10 На рисунке 1.10 показаны магнитное поле постоянного магнита. Линии магнитной индукции замыкаются в окружающем пространстве. |
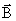не имеют ни начала, ни конца. Мы знаем, что поток любого вектора через поверхность равен разности числа линий, начинающихся у поверхности, и числа линий, оканчивающихся внутри поверхности:
.
,
(в интегральной форме): поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
,
– оператор Лапласа.
или 
Рис. 1.9
Не нашли, что искали? Воспользуйтесь поиском: