
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Объёмной плотностью
| W | B 2 | m m H 2 | BH | ||||||||||||||||
| w = | = | = | = | . | |||||||||||||||
| V | 2m m | ||||||||||||||||||
| Эти соотношения носят общий характер и справедливы и для неодно- | |||||||||||||||||||
| родных полей, но только для сред, | для которых связь между B | и H линейная | |||||||||||||||||
| (т. е. для пара- и диамагнетиков). | |||||||||||||||||||
| Выражение для объёмной плотности энергии магнитного поля аналогично | |||||||||||||||||||
| соответствующему | выражению для | объёмной плотности энергии электро- | |||||||||||||||||
| W | e 0 | e E 2 | ED | ||||||||||||||||
| статического поля: | w = | V | = | = | , | с той разницей, что электрические |
величины заменены в нём магнитными.
61. Волновое уравнение для электромагнитного поля
Иными словами, уберём из этих уравнений все заряды и токи. Для однородной и изотропной среды, не обладающей ферромагнитными и сегнетоэлектрическими свойствами (такая среда называется линейной, поскольку выполняется линейная связь между напряженностью и индукцией электрического и магнитного полей соответственно), получим:




Путём чисто математических преобразований, без каких-либо дополнительных предположений эти уравнения приводятся к виду:


А это есть ни что иное, как волновые уравнения для векторов напряженности электрического и магнитного полей. Мы знаем, что коэффициент в правой части уравнений есть обратный квадрат фазовой скорости волны; отсюда сразу находим эту скорость:
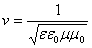
В вакууме e = m = 1, откуда получаем результат, весьма озадачивший современников Максвелла: скорость распространения электромагнитных волн в вакууме есть константа, не зависящая от системы отсчета (уравнения Максвелла, как известно, не инвариантны к преобразованиям Галилея):

Общее решение волнового уравнения нам известно. Частный случай этого решения - синусоидальные волны. Особенность электромагнитных волн в том, что решения для E и H дают одну волну с двумя составляющими; кроме того, колеблющиеся величины - векторные. Далее дадим краткую сводку свойств электромагнитных волн, непосредственно следующих из решения векторных волновых уравнений.
62. Плотность потока электромагнитной энергии. Вектор Умова-Пойнтинга
Плотность потока электромагнитного излучения – это отношение электромагнитной энергии ∆W, проходящей через перпендикулярную лучам поверхность площадью S, за время ∆t, к произведению S на ∆t.
J= ∆W/(S*∆t)
Единицей измерения плотности магнитного потока в систему СИ являются ватты на квадратный метр (Вт/м^2)
Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, один из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов: 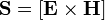
где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно. В этом случае чёткий физический смысл имеет только действительная часть комплексного вектора S — это вектор усреднённой за период плотности потока энергии. Физический смысл мнимой части зависит от конкретной задачи.
Модуль вектора Пойнтинга равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.
Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то нормальная составляющая вектора S непрерывна на границе двух сред.
63. Основные законы геометрической оптики
Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Опытным доказательством этого закона могут служить резкие тени, отбрасываемые непрозрачными телами при освещении светом источника достаточно малых размеров («точечный источник»). Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет. Следует отметить, что закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через малые отверстия, размеры которых сравнимы с длиной волны. Таким образом, геометрическая оптика, опирающаяся на представление о световых лучах, есть предельный случай волновой оптики при λ → 0. Границы применимости геометрической оптики будут рассмотрены в разделе о дифракции света.
На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а часть пройдет через границу и продолжит распространяться во второй среде.
Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α.
Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред:
|
Закон преломления был экспериментально установлен голландским ученым В. Снеллиусом в 1621 г.
Постоянную величину n называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.
Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления:
| n = n 2 / n 1. |
Законы отражения и преломления находят объяснение в волновой физике. Согласно волновым представлениям, преломление является следствием изменения скорости распространения волн при переходе из одной среды в другую. Физический смысл показателя преломления – это отношение скорости распространения волн в первой среде υ1 к скорости их распространения во второй среде υ2:

|
Абсолютный показатель преломления равен отношению скорости света c в вакууме к скорости света υ в среде:

|
64. Интерференция световых волн. Связь между разностью фаз и оптической разностью хода. Условия интерференционных максимумов и минимумов
При наложении двух когерентных световых волн происходит пространственное перераспределение световой энергии, в результате чего в одних местах возникают максимумы, а в других минимумы интенсивности, т.е. появляется интерференционная картина.
Δx - разность хода, т. е.. 
 - разность фаз.
- разность фаз.
Максимумы интенсивности появляются там, где, т.е. при  , где m=0,1,2,… Следовательно
, где m=0,1,2,… Следовательно 
Отсюда условие максимума:  , где m- порядок интерференционного максимума.
, где m- порядок интерференционного максимума.
Если разность хода равна целому числу длин волн или чётному числу полуволн, то будет наблюдаться максимум интенсивности при интерференции.
Условие минимума: если  , то
, то  , где m=0,1,2,…
, где m=0,1,2,…
Тогда  и
и 
Если разность хода равна нечётному числу полуволн, то в данной точке экрана будет наблюдаться минимум интенсивности при интерференции.
Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света.
Произведение геометрического пути волны на показатель преломления среды, т. е. хп, называют оптической длиной пути, а разность этих путей
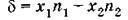
Не нашли, что искали? Воспользуйтесь поиском:
