Обратный эффект Комптона

Эффектом, обратным эффекту Комптона, является увеличение частоты света, претерпевающего рассеяние на релятивистских электронах, имеющих энергию выше, чем энергия фотонов. То есть в процессе такого взаимодействия происходит передача энергии от электрона фотону.

Энергия рассеянных фотонов определяется выражением^[2]:

где и 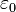— энергия рассеянного и падающего фотонов соответственно, K — кинетическая энергия электрона.

Обратный эффект Комптона ответственен за рентгеновское излучение галактических источников, рентгеновскую составляющую реликтового фонового излучения (эффект Сюняева — Зельдовича), трансформацию плазменных волн в высокочастотные электромагнитные волны

Первая попытка построения неклассической теории атома была предпринята датским физиком Н. Бором в 1913 году. Однако, в теории Н.Бора не содержалось принципиального отказа от классических пред­ставлений модели Резерфорда, не были введены ограничения, накладываемые на состояние электрона в атоме. Модель атома принципиально строится на постулатах, сформулированных Бором.

Первый постулат Бора: существуют некоторые стационарные состояния атома, находясь в которых он не излучает и не поглощает энергии.

Второй постулат Бора: атом излучает или поглощает один квант энергии при переходе из одного стационарного состояния в другое. Этот постулат представляет собой правило частот, которое можно сфор­мулировать следующим образом: при переходе атома из одного стацио­нарного состояния в другое излучается или поглощается квант энергии равный разности энергий стационарных состояний, т.е.

. (13.23)

Третий постулат Бора: электрон в стационарном состоянии атома движется по таким круговым орбитам, на которых момент импульса электрона кратен постоянной Планка, т.е. удовлетворяет условию

, (13.24)

где – масса электрона, – скорость электрона, – радиус орбиты электрона, , целое число, определяющее номер энергетического уровня атома водорода, называе­мое главным квантовым числом.

Полная энергия электрона в атоме водорода

. (13.25)

Таким образом, представления Бора об атоме водорода позволили определить размеры атома. При = I имеем

м. (13.26)

Эту величину называют радиусом первой орбиты атома водорода (ради­ус первой боровской орбиты).

Гипотеза де Бройля. Ранее мы установили, что свет обладает одновременно и свойствами непрерывной достаточно протяженной волны и свойствами частиц (фотонов), т.е. имеет дискретную (прерывистую структуру), эти противоположные свойства составляют единство в световой волне, что позволяет говорить о корпускулярно-волновом дуализме свойств световой волны. В проявлении этих противоположных свойств имеется определенная закономерность: с уменьшением длины волны (увеличением частоты) все более отчетливей проявляются квантовые свойства света. В 1924 году французский физик Луи де Бройль пришел к выводу о том, что корпускулярно-волновая природа характерна не только для электромагнитных волн, но и для любых движущихся частиц вещества. Выражение для им­пульса фотона 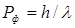дe Бройль обобщил для любых волновых процессов, связанных с движущимися частицами, обладающими импульсом . Длина волны де Бройля равна

(14.1)

Формула (14.1) называется формулой де Бройля и является одной из важнейших в современной физике. Для частицы с массой , движущейся со скоростью , имеем

. (14.2)

Если частица имеет кинетическую энергию Е, то учитывая связь импульса и энергии, можно записать (14.2) в форме

. (14.3)

Следует отметить, что волны де Бройля не являются электромагнитными. Они имеют особую природу, не имеющую аналогии в классической физике. Причем волны де Бройля представляют собой универсальное яв­ление для всех движущихся частиц.

Гипотеза де Бройля экспериментально подтвердилась в опытах К. Дэвиссона и Л. Джермера в 1927 году, наблю­давших рассеяние электронов монокристаллом никеля. В экспериментах по рассеянию электронов на кристаллах обнаруживается, что в отдельных направлениях рассеивается большее число электронов, чем во всех других. С волновой точки зрения наличие максимумов числа электронов в некоторых направлениях означает, что в этих направлениях волны де Бройля имеют наибольшую интенсивность. Учитывая, что интенсивность волны пропорциональна квадрату модуля амплитуды волны, можно дать своеобразное вероятностное толкование волн де Бройля. Квадрат модуля ½А½² амплитуды волн де Бройля в данной точке пространства является мерой вероятности того, что частица находится в этой точке. Для описания распределения вероятности нахождения частицы в данный момент времени в некоторой области пространства вводится функция координат и времени, которую называют волновой функцией . 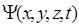Волновая функция сама по себе физического смысла не имеет, смысл имеет квадрат модуля волновой функции. Вероятность нахождения частицы в объеме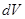

, (14.4)

где волновая функция, описывающая состояние частицы; функция, комплексно сопряженная с 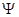; квадрат модуля волновой функции является плотностью вероятности нахождения частицы в данной точке простран­ства. Иными словами, величина 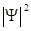определяет интенсивность волн де Бройля. По определению волновой функции она должна удовлетворять следующему условию

, (14.5)

где тройной интеграл вычисляется по всему пространству от -¥ до ¥. Выражение (14.5) означает, что нахождение частицы в какой либо точке всего бесконечного пространства есть достоверное событие и его вероятность должна быть равна единице. Выражение (14.5) называют также условием нормировки волновой функции или условием нормировки вероятностей.

Не нашли, что искали? Воспользуйтесь поиском: