Оптической разностью хода волн.

На основании этого получим связь между разностью фаз и оптической разностью хода интерферирующих волн:

65. Интерференция света в тонких пленках

Интерференционные полосы равного наклона. При освещении тонкой пленки происходит наложение волн от одного и того же источника, отразившихся от передней и задней поверхностей пленки. При этом может возникнуть интерференция света. Если свет белый, то интерференционные полосы окрашены. Интерференцию в пленках можно наблюдать на стенках мыльных пузырей, на тонких пленках масла или нефти, плавающих на поверхности воды, на пленках, возникающих на поверхности металлов или зеркала.

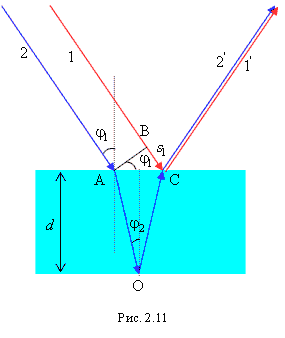Рассмотрим сначала плоскопараллельную пластинку толщины с показателем преломления 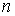(рис. 2.11). Пусть на пластинку падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей. Пластинка отбрасывает вверх два параллельных пучка света, один из которых образовался за счет отражения от верхней поверхности пластинки, второй – вследствие отражения от нижней поверхности. Каждый из этих пучков представлен на рис. 2.11 только одним лучом.

При входе в пластинку и при выходе из нее пучок 2 претерпевает преломление. Кроме двух пучков 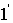и , пластинка отбрасывает вверх пучки, возникающие в результате трех-, пяти- и т.д. кратного отражения от поверхностей пластинки. Однако ввиду малой интенсивности их можно не принимать во внимание.

Рассмотрим интерференцию лучей, отраженных от пластинки. Поскольку на пластинку падает плоская волна, то фронт этой волны представляет собой плоскость, перпендикулярную лучам 1 и 2. На рис. 2.11 прямая ВС представляет собой сечение волнового фронта плоскостью рисунка. Оптическая разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, будет

,

(2.13)

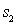где – длина отрезка ВС, а – суммарная длина отрезков АО и ОС. Показатель преломления среды, окружающей пластинку, полагаем равным единице. Из рис. 2.11 видно, что , . Подстановка этих выражений в (2.13) дает 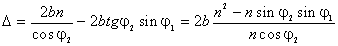. Воспользуемся законом преломления света: ; и учтем, что , тогда для разности хода получим следующее выражение: .

При вычислении разности фаз между колебаниями в лучах и нужно, кроме оптической разности хода D, учесть возможность изменения фазы при отражении в точке С. В точке С отражение волны происходит от границы раздела среды оптически менее плотной со средой оптически более плотной. Поэтому фаза волны претерпевает изменение на p. В точке отражение происходит от границы раздела среды оптически более плотной со средой оптически менее плотной, и скачка фазы в этом случае не происходит. Качественно это можно представить себе следующим образом. Если толщину пластинки устремить к нулю, то полученная нами формула для оптической разности хода дает . Поэтому при наложении лучей и должно происходить усиление колебаний. Но это невозможно, так как бесконечно тонкая пластинка вообще не может оказывать влияния на распространение света. Поэтому волны, отраженные от передней и задней поверхности пластинки, должны при интерференции гасить друг друга. Их фазы должны быть противоположны, то есть оптическая разность хода D при d →0 должна стремиться к . Поэтому к прежнему выражению для D нужно прибавить или вычесть , где λ₀ – длина волны в вакууме. В результате получается:

.

(2.14)

Итак, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется формулой (2.14). Эти волны могут интерферировать, если оптическая разность хода не превышает длину когерентности. Последнее требование для солнечного излучения приводит к тому, что интерференция при освещении пластинки наблюдается только в том случае, если толщина пластинки не превышает нескольких сотых миллиметра.

72) Закон Малюса. Свет называют поляризованным, если направления светового вектора упорядочены каким–либо образом. В естественном свете эти направления изменяются случайным образом. Такой свет называют неполяризованным.

Степень поляризации определяется выражением:

.

Если неполяризованный свет проходит через поляризатор, он становится линейно – или плоскополяризованным светом

Схема получения лоскополяризованного света.

При этом, очевидно, и степень поляризации равна единице. Для естественного света и .

73) Поляризация при отражении и преломлении. Двойное лучепреломление. Когда световая волна проходит через границу раздела двух сред, то при этом происходит частичное отражение световой волны.

Шотландский физик Д.Брюстер (1781 – 1868) установил закон, согласно которому при угле падения 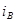(угол Брюстера), определяемого соотношением

,

Схема поляризации отраженного и преломленного лучей

74)Лучеиспускательная способность тела – энергия ЭМ излучения dW_изл, испускаемая единицей площади поверхности тела за единицу времени в интервале частот от ν до . Таким образом

Единица измерения лучеиспускательной способности в СИ равна Дж/м².

Спектральной характеристикой поглощения телом ЭМ волн является поглощательная способность тела A(ν,T). Поглощательная способность показывает долю падающей на единицу площади поверхности тела за единицу времени энергии dW, поглощаемой телом в интервале частот от ν до ν+dν, т.е.

Замкнутая полость

Две пластины.

Закон Кирхгофа: Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока

Первое правило

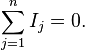
Сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментальногозакона сохранения заряда.

Второе правило

для постоянных напряжений

для переменных напряжений

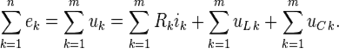
На основе анализа опытных данных Д. Стефан пришел к заключению, что энергетическая светимость любого тела прямо пропорциональна четвертой степени абсолютной температуры. Л. Больцман в 1884г. теоретически показал, что это утверждение справедливо только для АЧТ. Эта зависимость вошла в историю физики как закон Стефана-Больцмана

,

Коэффициент пропорциональности (Вт/м²×К⁴) называется постоянной Стефана-Больцмана.

Нахождение явного вида функции Кирхгофа был предпринято В. Вином в 1897г., который рассмотрел задачу об адиабатическом сжатии излучения АЧТ в цилиндрическом сосуде с подвижным зеркальным поршнем и зеркальными стенками. Вин получил следующее выражение для функции Кирхгофа:

где - некоторая неизвестная в явном виде функция.

В. Вин не установил явного вида функции, однако, из формулы Вина (13.9) вытекает закон Стефана-Больцмана.

Из опытов было известно, что зависимость лучеиспускательной способности АЧТ от частоты при различных температурах имеет вид, показанный на рисунке. Из рисунка видно, что с ростом температуры

	увеличивается максимум лучеиспускательной способности АЧТ.
Рисунок 13.3 Зависимость Е(ν,T) для АЧТ от ν

,

λ_мах- длина волны, соответствующая максимуму лучеиспускательной способности АЧТ. Этот максимум с ростом температуры смещается в сторону коротких длин волн. Постоянная м×К называется постоянной Вина и определяется опытным путем.

Второй закон Вина: максимум лучеиспускательной способности АЧТ прямо пропорционален пятой степени абсолютной температуры:

.

где Вт/(м⁷×К⁵) - постоянная второго закона Вина.

76) Планк установил, что энергия кванта должна быть равна , где h - постоянная Планка. Дж×с. Окончательное выражение для функции Кирхгофа Планк получил в виде:

. (13.15)

Формула Планка для лучеиспускательной способности АЧТ хорошо согласуется с опытом при различных температурах. Согласно гипотезе Планка о квантовом характере излучения, свет имеет дискретную, прерывистую структуру, т.е. обладает корпускулярными свойствами. Кванты ЭМ излучения были названы фотонами, обладающими свойствами частиц.

Рассматривая ЭМ излучение (свет) как поток фотонов, движущихся со скоростью света, найдем массу и импульс фотона.

77)Фотоны - это кванты света. Фотоны не имеют массы покоя и электрического заряда, стабильны. Спин фотона равен 1.

Фотон означает свет (от греч.).

Согласно закону пропорциональности массы и энергии и гипотезе Планка, энергия фотона определяется формулой:

Фотоныимеют импульс:

Энергия фотона равна . Согласно релятивистской механике энергию фотона можно представить в виде . Сравнивая эти выражения, найдем массу фотона:

.

Масса фотона зависит только от частоты световой волны (от «цвета» фотона).

Импульс фотона будет равен:

.

Эффе́кт Ко́мптона (Ко́мптон-эффе́кт, ко́мптоновское рассе́яние) — некогерентное рассеяние фотонов на свободных электронах, некогерентность означает, что фотоны до и после рассеяния не интерферируют. Эффект сопровождается изменением частоты фотонов, часть энергии которых после рассеяния передается электронам.

При рассеянии фотона на свободном электроне частоты фотона и 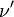(до и после рассеяния соответственно) связаны соотношением:

где — угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).

Перейдя к длинам волн:

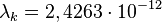где — комптоновская длина волны электрона, равная м.

Уменьшение энергии фотона в результате комптоновского рассеяния называется комптоновским сдвигом. Объяснение эффекта Комптона в рамках классической электродинамики невозможно, так как рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не меняет её частоты.

Эффект Комптона является одним из доказательств справедливости корпускулярно-волнового дуализма микрочастиц и подтверждает существование фотонов.

Закон сохранения энергии в эффекте Комптона в случае рассеяния на покоящемся электроне, можно записать следующим образом^[1]:

Не нашли, что искали? Воспользуйтесь поиском: