
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Приведение системы дифференцированных уравнений для заданной вероятностной модели предприятия.
Рассмотрим решение системы дифференциальных уравнений построенной по вероятностной модели предприятия УП «Проектный институт Гродногипрозем». Данная модель примет вид на рис.1.2.

|

|

|

|

|

|

|

|
Рис.1.2. Модель обслуживания заявок в УП «Проектный институт Гродногипрозем».
Где система  ― приемная. Обработка поступающих заявок.
― приемная. Обработка поступающих заявок.
Система  ― производственный отдел №1.Обслуживаются заявки, поступившие из Гродненского, Щучинского, Берестовикого района.
― производственный отдел №1.Обслуживаются заявки, поступившие из Гродненского, Щучинского, Берестовикого района.
Система  ― производственный отдел №2. Обработка заявок, поступивших из Волковыского, Свислочского, Мостовского района.
― производственный отдел №2. Обработка заявок, поступивших из Волковыского, Свислочского, Мостовского района.
Система  ― производственный отдел №3. Обработка заявок, поступивших из Слонимского, Зельвенского, Дятловского района.
― производственный отдел №3. Обработка заявок, поступивших из Слонимского, Зельвенского, Дятловского района.
Система  ― производственный отдел №4. Обслуживаются заявки, поступившие из Лидского, Вороновского, Ивьевского, Новогрудского района.
― производственный отдел №4. Обслуживаются заявки, поступившие из Лидского, Вороновского, Ивьевского, Новогрудского района.
Система  ― производственный отдел №5. Обслуживаются заявки, поступившие из Сморгонского, Островецкого, Ошмянского, Корелического района.
― производственный отдел №5. Обслуживаются заявки, поступившие из Сморгонского, Островецкого, Ошмянского, Корелического района.
Система  ― расчетно-сметная группа. В обязанности входит: составление сметы работы, заключение договора с клиентом.
― расчетно-сметная группа. В обязанности входит: составление сметы работы, заключение договора с клиентом.
В рассматриваемой модели за единицу времени возьмем одну неделю. Под заявкой в системах  будем понимать заявление на услугу предприятия. В системе
будем понимать заявление на услугу предприятия. В системе  под заявкой понимается договор заключенный с предприятием и клиентом на оказание услуг предприятия. Под СМО
под заявкой понимается договор заключенный с предприятием и клиентом на оказание услуг предприятия. Под СМО  понимаются отделы предприятия, оказывающие услуги населению.
понимаются отделы предприятия, оказывающие услуги населению.
Система обыкновенных линейных дифференциальных уравнений с разрывными правыми частями описанная в главе 1 пункт 1.2 примет вид:
 (1.7)
(1.7)
Определим явную форму уравнений (1.7) в областях линейности их правых частей, тогда приходим к системе (1.6), при  :
:

где 
 Здесь
Здесь  непересекающиеся множества индексов компонент вектора
непересекающиеся множества индексов компонент вектора

Причем при фиксированном  число всевозможных разбиений множества индексов компонент этого вектора
число всевозможных разбиений множества индексов компонент этого вектора  равно
равно  Система (1.7) решается в каждой из областей разбиения фазового пространства:
Система (1.7) решается в каждой из областей разбиения фазового пространства:


 и т.д.
и т.д.
Для нахождения среднего относительного числа заявок необходимо рассмотреть систему (1.7) в области  , где она примет вид при
, где она примет вид при  :
:
 (1.8)
(1.8)
Исследуем, работу предприятия на интервале времени  . Предположим, что интенсивности поступления заявок каждого из типов с учетом времени года описываются функциями вида:
. Предположим, что интенсивности поступления заявок каждого из типов с учетом времени года описываются функциями вида:
 (1.9)
(1.9)
На интервале времени  система уравнений (1.8) превращается в систему линейных неоднородных дифференциальных уравнений с постоянными коэффициентами:
система уравнений (1.8) превращается в систему линейных неоднородных дифференциальных уравнений с постоянными коэффициентами:
 (1.10)
(1.10)
Следовательно, на интервале  вид системы ДУ аналогичен (1.10), если заменить в ней
вид системы ДУ аналогичен (1.10), если заменить в ней  на
на  Для интервала
Для интервала  вид системы ДУ будет аналогичен (1.10), если заменить в ней
вид системы ДУ будет аналогичен (1.10), если заменить в ней  на
на  Аналогичным образом поступаем и для интервала
Аналогичным образом поступаем и для интервала  в ДУ (1.10) заменяем
в ДУ (1.10) заменяем  на
на 
Решение системы (1.10) с начальным условием  производится в программе Wolfram Mathematica 7.0.
производится в программе Wolfram Mathematica 7.0.
Для того чтобы система (1.10) находилась в области  на интервале
на интервале  , необходимо выполнение неравенств:
, необходимо выполнение неравенств:
 (1.11)
(1.11)
При изменении интенсивности  в момент времени
в момент времени  возможны следующие случаи:
возможны следующие случаи:
1)  удовлетворяет неравенствам (1.11), т.е. система остается в области
удовлетворяет неравенствам (1.11), т.е. система остается в области  .
.
2)  не удовлетворяет (1.11) – произошел переход другую область.
не удовлетворяет (1.11) – произошел переход другую область.
3)  удовлетворяет неравенствам (1.11), т.е. система остается в области
удовлетворяет неравенствам (1.11), т.е. система остается в области  .
.
4)  не удовлетворяет (1.11) – произошел переход другую область.
не удовлетворяет (1.11) – произошел переход другую область.
5)  удовлетворяет неравенствам (1.11), т.е. система остается в области
удовлетворяет неравенствам (1.11), т.е. система остается в области  .
.
6)  не удовлетворяет (1.11) – произошел переход другую область.
не удовлетворяет (1.11) – произошел переход другую область.
 .
.
Для решения поставленной задачи (1.10) на интервале  , когда система остается в области
, когда система остается в области  . Система уравнений в этом случае будет иметь вид (1.10), если заменить
. Система уравнений в этом случае будет иметь вид (1.10), если заменить  соответственно на
соответственно на  . Начальными условиями для нее будут
. Начальными условиями для нее будут  . Для того чтобы система находилась в области
. Для того чтобы система находилась в области  на временном интервале
на временном интервале  , необходимо выполнение условий:
, необходимо выполнение условий:
 .
.
Осталось рассмотреть решение задачи (1.10) на интервале  , когда система останется в области
, когда система останется в области  . Система будет иметь вид (1.10), если заменить
. Система будет иметь вид (1.10), если заменить  соответственно на
соответственно на  . Начальными условиями для нее будут
. Начальными условиями для нее будут  . Для того чтобы система находилась в области
. Для того чтобы система находилась в области  на временном интервале
на временном интервале  , необходимо выполнение условий:
, необходимо выполнение условий:
 .
.
Решение системы производится в программе Wolfram Mathematica 7.0 [ПРИЛОЖЕНИЕ].
1.4. Нахождение среднего относительного числа заявок на примере УП «Проектный институт Гродногипрозем»
В предприятие поступило за год  заявок от физических лиц за 2015 год. В рассматриваемой модели за единицу времени возьмем одну неделю. Функционирование предприятия УП «Проектный институт Гродногипрозем» описывается следующими параметрами:
заявок от физических лиц за 2015 год. В рассматриваемой модели за единицу времени возьмем одну неделю. Функционирование предприятия УП «Проектный институт Гродногипрозем» описывается следующими параметрами:

Исследуя работу предприятия за год, интенсивность поступления заявок каждого из типов с учетом времени года описывается функцией вида (1.9):


На интервале  рассматривается работа предприятия за осенний период. За интервал времени
рассматривается работа предприятия за осенний период. За интервал времени  берем работу предприятия на зимний период. На интервале
берем работу предприятия на зимний период. На интервале  рассматривается работа предприятия за весенний период, а под интервалом
рассматривается работа предприятия за весенний период, а под интервалом  рассмотрим работу за летний период. Найдем среднее относительное число заявок в области
рассмотрим работу за летний период. Найдем среднее относительное число заявок в области  . Для решения системы (1.10) найдем линию обслуживания
. Для решения системы (1.10) найдем линию обслуживания  где
где  количество сотрудников в производственном отделе №2.
количество сотрудников в производственном отделе №2.
Решение системы (1.10) на интервале  примет вид на рис. 1.3-1.9:
примет вид на рис. 1.3-1.9:
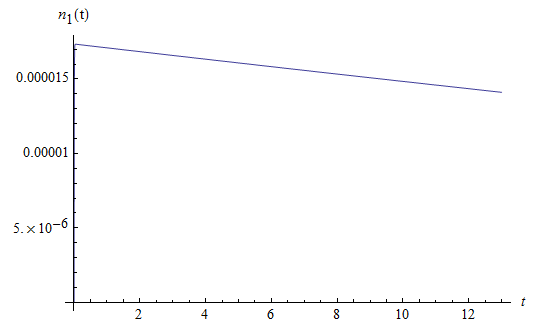
Рис. 1.3. Среднее число заявок  , находящихся на интервале времени
, находящихся на интервале времени 
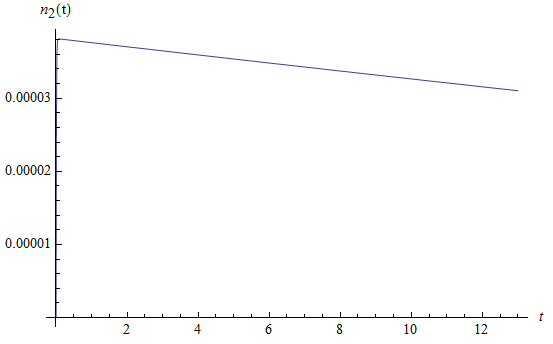
Рис. 1.4. Среднее число заявок  первого типа, находящихся на интервале времени
первого типа, находящихся на интервале времени 
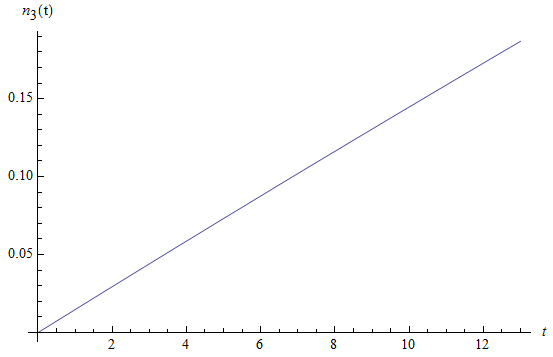
Рис. 1.5. Среднее число заявок  второго типа, находящихся на интервале времени
второго типа, находящихся на интервале времени 
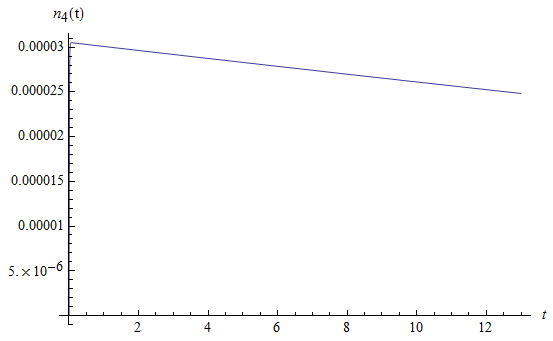
Рис. 1.6. Среднее число заявок  третьего типа, находящихся на интервале времени
третьего типа, находящихся на интервале времени 
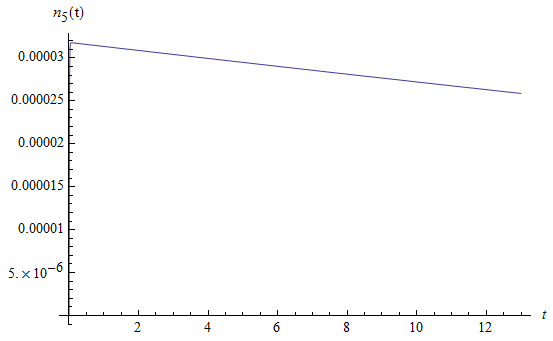
Рис. 1.7. Среднее число заявок  четвертого типа, находящихся на интервале времени
четвертого типа, находящихся на интервале времени 
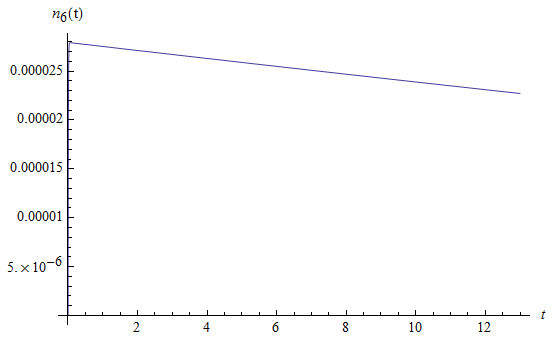
Рис. 1.8. Среднее число заявок  пятого типа, находящихся на интервале времени
пятого типа, находящихся на интервале времени 
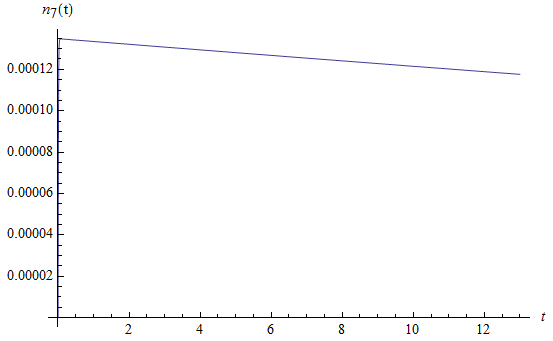
Рис. 1.9. Среднее число заявок  , находящихся на интервале времени
, находящихся на интервале времени 
Аналогично решается (1.10) для остальных интервалов времени только  заменяется на соответствующее значение для интервала
заменяется на соответствующее значение для интервала  .
.
ГЛАВА 2. НАХОЖДЕНИЕ ОЖИДАЕМОГО ДОХОДА ЦЕНТРАЛЬНОЙ ЗАМКНУТОЙ СЕТИ ДЛЯ СЛУЧАЯ, КОГДА ДОХОДЫ ОТ ПЕРЕХОДОВ ЗАЯВОК МЕЖДУ СИСТЕМАМИ СЕТИ ЯВЛЯЮТСЯ СВ С ЗАДАННЫМИ МОМЕНТАМИ ПЕРВЫХ ДВУХ ПОРЯДКОВ
2.1. Нахождение ожидаемых доходов в центральной системе 
Рассмотрим замкнутую сеть массового обслуживания с разнотипными заявками, которая является вероятностной моделью обслуживания заявок в УП «Проектный институт Гродногипрозем», рис.1.1.
Допустим, что  заявка типа
заявка типа  требуемой обслуживания,
требуемой обслуживания,  . Системами
. Системами  в данной сети будут отделы предприятия, которые занимаются приемом и обслуживанием заявок граждан Гродненской области. Число линий обслуживания
в данной сети будут отделы предприятия, которые занимаются приемом и обслуживанием заявок граждан Гродненской области. Число линий обслуживания  , в системах соответствуют сотрудникам, которые выполняют заявку.
, в системах соответствуют сотрудникам, которые выполняют заявку.
Состояние сети описывается вектором  где
где  число заявок находящихся в момент времени
число заявок находящихся в момент времени  в системе
в системе  .
.
Заявка при переходе из одной СМО в другую приносит последней системе некоторый случайный доход и соответственно доход первой системы уменьшается на эту случайную величину.
Рассмотрим динамику изменения доходов некоторой системы  сети. Обозначим через
сети. Обозначим через  ее доход в момент времени
ее доход в момент времени  .
.
Пусть в начальный момент времени доход системы равен  . Доход этой СМО в момент времени
. Доход этой СМО в момент времени  можно представить в виде
можно представить в виде  , где
, где  -изменение дохода системы
-изменение дохода системы  на интервале времени
на интервале времени  . Для нахождения этой величины выпишем условные вероятности событий, которые могут произойти за время
. Для нахождения этой величины выпишем условные вероятности событий, которые могут произойти за время  , и изменения доходов системы
, и изменения доходов системы  , связанные с этими событиями.
, связанные с этими событиями.
1. С вероятностью  заявка из системы
заявка из системы  перейдет во внешнюю среду, при этом доход системы
перейдет во внешнюю среду, при этом доход системы  уменьшится на величину
уменьшится на величину  , где
, где  - СВ с МО
- СВ с МО  ,
,  - функция Хевисайда.
- функция Хевисайда.
2. С вероятностью  заявка перейдет из
заявка перейдет из  в систему
в систему  , при этом доход системы
, при этом доход системы  возрастет на величину
возрастет на величину  , а доход системы
, а доход системы  уменьшается на эту величину, где
уменьшается на эту величину, где  - СВ с МО
- СВ с МО  ,
,  - вероятность перехода заявки из системы
- вероятность перехода заявки из системы  в систему
в систему  .
.
3. С вероятностью  заявка из системы
заявка из системы  перейдет в систему
перейдет в систему  , при этом доход СМО
, при этом доход СМО  уменьшится на величину
уменьшится на величину  , а доход системы
, а доход системы  возрастет на эту величину, где
возрастет на эту величину, где  - СВ с МО
- СВ с МО  .
.
4. С вероятностью
 на отрезе времени
на отрезе времени  изменение состояния системы
изменение состояния системы  не произойдет.[4]
не произойдет.[4]
Кроме того, за каждый промежуток времени  система
система  увеличивает свой доход на величину
увеличивает свой доход на величину  , где
, где  СВ с МО
СВ с МО  . Будем также считать, что СВ
. Будем также считать, что СВ  независимы по отношению к СВ
независимы по отношению к СВ  . Очевидно, что
. Очевидно, что  . Тогда вышеуказанное примет вид:
. Тогда вышеуказанное примет вид:
 (2.1)
(2.1)
При фиксированной реализации процесса  , учитывая (2.1), можно записать:
, учитывая (2.1), можно записать:

Усредняя по  с учетом условий нормировки
с учетом условий нормировки  для изменения ожидаемого дохода системы
для изменения ожидаемого дохода системы  получаем
получаем

Пусть система  содержит
содержит  идентичных линий обслуживания, в каждой из которых время обслуживания заявок распределено по показательному закону с параметром
идентичных линий обслуживания, в каждой из которых время обслуживания заявок распределено по показательному закону с параметром  . В этом случае
. В этом случае

В качестве аппроксимации среднего значения выражения  возьмем
возьмем  , т.е. воспользуемся приближенным равенством
, т.е. воспользуемся приближенным равенством
 ,
,
где  - среднее число заявок (ожидающих и обслуживающихся) в системе
- среднее число заявок (ожидающих и обслуживающихся) в системе  в момент времени
в момент времени  . С учетом этого равенства поучаем следующее приближенное соотношение:
. С учетом этого равенства поучаем следующее приближенное соотношение:
 (2.2)
(2.2)
Введем обозначение  . Из (2.1) и (2.2) получаем
. Из (2.1) и (2.2) получаем

Далее, переход к пределу при  получим неоднородные линейные ОДУ первого порядка:
получим неоднородные линейные ОДУ первого порядка:
 (2.3)
(2.3)
Интегрируя данные ОДУ (2.3) при начальных условиях  можно найти ожидаемые доходы систем сети по формуле[1]:
можно найти ожидаемые доходы систем сети по формуле[1]:
 (2.4)
(2.4)
2.2. Нахождение ожидаемых доходов в УП «Проектный институт Гродногипрозем»
Распишем(2.4) для сети УП «Проектный институт Гродногипрозем» для центральной системы  . С учетом того, что,
. С учетом того, что,  и
и  , остальные
, остальные  , то формула для нахождения ожидаемого дохода для центральной системы примет вид
, то формула для нахождения ожидаемого дохода для центральной системы примет вид

Полученные в главе 1 подпункте 1.4 среднее относительное число заявок используем для нахождения дохода. Интенсивность обслуживания заявок в отделах равны 

Количество сотрудников в отделах равно 
 .
.
В табл. 2.1.-2.4. приведен средний доход предприятия от удовлетворения заявок от физических лиц. Отдел расчетно-сметной получает доход в размере  млн. бел. руб., когда заключает договор с заказчиком, т.е. при переходе заявки из расчетно-сметной группы во внешнюю среду. Так как основные затраты, связанные с удовлетворением заявки, поступающих из производственных отделов №1-5, заложены в себестоимость продукции – расчетно-сметная группа не несет дополнительных расходов.
млн. бел. руб., когда заключает договор с заказчиком, т.е. при переходе заявки из расчетно-сметной группы во внешнюю среду. Так как основные затраты, связанные с удовлетворением заявки, поступающих из производственных отделов №1-5, заложены в себестоимость продукции – расчетно-сметная группа не несет дополнительных расходов.
Таблица 2.1
Средний доход предприятия за 
| Производственный отдел №1 | Производственный отдел №2 | Производственный отдел №3 | Производственный отдел №4 | Производственный отдел №5 | |
| Неделя, млн. бел. руб | 55.08 | 61.03 | 21.56 | 75.09 | 68.68 |
| 1 заявка млн. бел. руб | 1.05 | 1.08 | 1.13 | 1.074 | 1.08 |
Используя данные, представленные в табл. 2.1 и программу, разработанную в пакете WolframMathematica [ПРИЛОЖЕНИЕ], получим график ожидаемого дохода для расчетно-сметового отдела при начальных  на интервале времени
на интервале времени  .
.
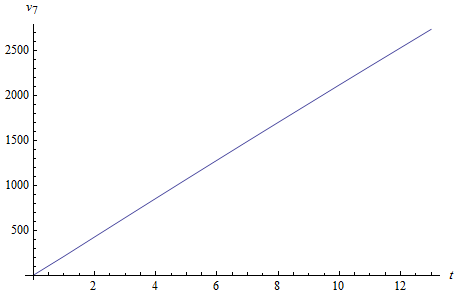
Рис. 2.1. График ожидаемого дохода  на интервале
на интервале 
Таблица 2.2
Средний доход предприятия за 
| Производственный отдел №1 | Производственный отдел №2 | Производственный отдел №3 | Производственный отдел №4 | Производственный отдел №5 | |
| Неделя, млн. бел. руб | 54.78 | 72.64 | 26.98 | 66.22 | 64.07 |
| 1 заявка млн. бел. руб | 1.25 | 1.2 | 1.2 | 1.16 | 1.18 |
Используя данные, представленные в табл. 2.2 и программу, разработанную в пакете WolframMathematica, получим график ожидаемого дохода для расчетно-сметового отдела  на интервале времени
на интервале времени  .
.
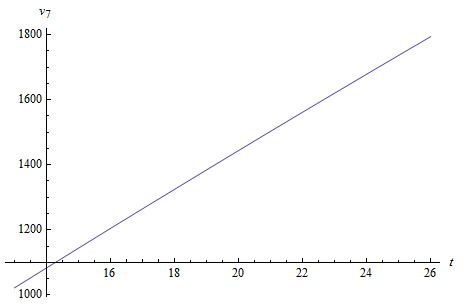
Рис. 2.2. График ожидаемого дохода  на интервале
на интервале 
Таблица 2.3
Средний доход предприятия за 
| Производственный отдел №1 | Производственный отдел №2 | Производственный отдел №3 | Производственный отдел №4 | Производственный отдел №5 | |
| Неделя, млн. бел. руб | 70.4 | 82.998 | 35.24 | 74.65 | 62.29 |
| 1 заявка млн. бел. руб | 1.08 | 1.1 | 1.13 | 1.08 | 1.13 |
Используя данные, представленные в табл. 2.3 и программу, разработанную в пакете WolframMathematica, получим график ожидаемого дохода для расчетно-сметового отдела  на интервале времени
на интервале времени  .
.
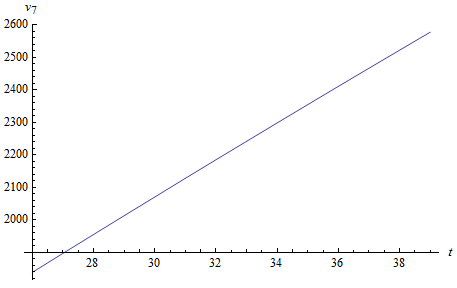
Рис. 2.3. График ожидаемого дохода  на интервале
на интервале 
Таблица 2.4
Средний доход предприятия за 
| Производственный отдел №1 | Производственный отдел №2 | Производственный отдел №3 | Производственный отдел №4 | Производственный отдел №5 | |
| Неделя, млн. бел. руб | 71.55 | 72.34 | 25.73 | 83.91 | 68.56 |
| 1 заявка млн. бел. руб | 1.02 | 1.04 | 1.06 | 1.07 | 1.05 |
Используя данные, представленные в табл. 2.4 и программу, разработанную в пакете WolframMathematica, получим график ожидаемого дохода для расчетно-сметового отдела  на интервале времени
на интервале времени  .
.
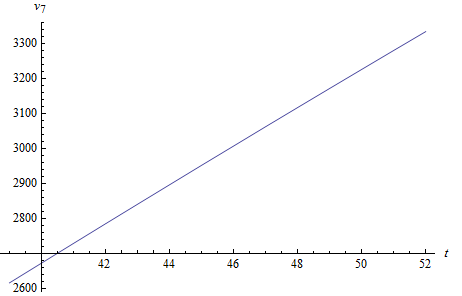
Рис. 2.4. График ожидаемого дохода  на интервале
на интервале 
Ожидаемый доход и реальный доход за год будет иметь вид рис. 2.5.
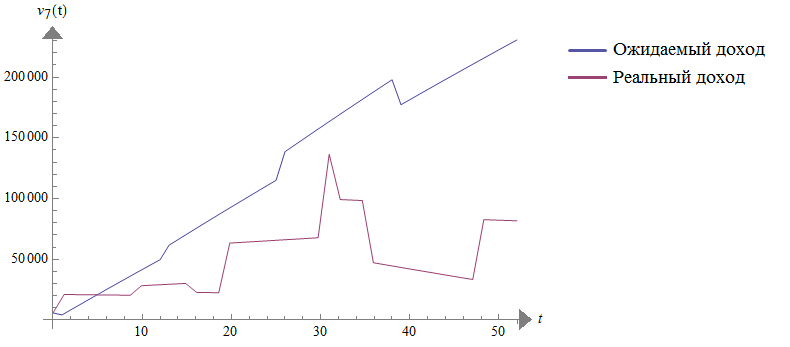
Рис. 2.5. График ожидаемого дохода за год 
По рис. 2.5. можем сделать вывод, что ожидаемый доход приближен к реальному доход осенью, зимой, весной. Реальный доход в летний период снижается.
ГЛАВА 3. ПОСТАНОВКА И РЕШЕНИЕ ОПТИМИЗАЦИОННОЙ ЗАДАЧИ ДЛЯ УП «ПРОЕКТНЫЙ ИНСТИТУТ ГРОДНОГИПРОЗЕМ»
3.1. Постановка оптимизационной задачи для УП «Проектный институт Гродногипрозем»
Рассмотрим замкнутую сеть массового обслуживания с разнотипными заявками, которая является вероятностной моделью обслуживания заявок в УП «Проектный институт Гродногипрозем», рис.1.1.
Допустим, что  заявка типа
заявка типа  требуемой обслуживания,
требуемой обслуживания,  . Системами
. Системами  в данной сети будут отделы предприятия, которые занимаются приемом и обслуживанием заявок граждан Гродненской области. Число линий обслуживания
в данной сети будут отделы предприятия, которые занимаются приемом и обслуживанием заявок граждан Гродненской области. Число линий обслуживания  , в системах соответствуют сотрудникам, которые выполняют заявку.
, в системах соответствуют сотрудникам, которые выполняют заявку.
В рассматриваемой модели за единицу времени возьмем одну неделю. Сформулируем оптимизационную задачу для нахождения оптимального числа линий обслуживания в системах сети при максимальном доходе сети в целом.

где  максимальное возможное количество линий обслуживаний,
максимальное возможное количество линий обслуживаний,  затраты на содержание одной заявки в
затраты на содержание одной заявки в  ой СМО (в очереди и на обслуживании),
ой СМО (в очереди и на обслуживании),  затраты на содержание одной линии обслуживания. Она решена методом полного перебора по
затраты на содержание одной линии обслуживания. Она решена методом полного перебора по  , а интегралы в выражениях можно вычислить последовательно применив два раза метод трапеций.
, а интегралы в выражениях можно вычислить последовательно применив два раза метод трапеций.
3.2. Решение оптимизационной задачи на примере УП «Проектный институт Гродногипрозем»
Про анализируя данные за год делает вывод, что максимально возможное количество сотрудников в отделах равны
 .
.
Затраты на содержание одной заявки (в очереди и на обслуживание) в отделах составляет  , затраты на содержание одного сотрудника в отделах равно
, затраты на содержание одного сотрудника в отделах равно  млн. бел. руб.
млн. бел. руб.
Поскольку на интервалах времени  функция
функция  принимает различные значения, то оптимальные числа сотрудников предприятия
принимает различные значения, то оптимальные числа сотрудников предприятия  будут различные для этих временных интервалов. Обозначим их
будут различные для этих временных интервалов. Обозначим их  для интервалов
для интервалов  соответственно.
соответственно.
Из-за того, что среднее относительное число заявок зависит от  , то при изменении
, то при изменении  будет пересчитываться система (1.10). Аналогично будет пересчитываться ожидаемый доход.
будет пересчитываться система (1.10). Аналогично будет пересчитываться ожидаемый доход.
Для решения поставленной задачи используем программу разработанную в WolframMathematica 7.0. Листинг программы в приложение. Решение на интервале  примет вид:
примет вид:
 .
.
Решение на интервале времени  примет вид:
примет вид:

Решение на интервале времени  примет вид:
примет вид:

Решение на интервале времени  примет вид:
примет вид:

ЗАКЛЮЧЕНИЕ
В дипломной работе была построена сетевая вероятностная модель обработки заявок в УП «Проектный институт Гродногипрозем». На основе построенной сетевой вероятностной модели обработки заявок в УП «Проектный институт Гродногипрозем» было построено ОДУ для среднего относительного числа заявок в системе сети. С помощью диффузионной аппроксимации были рассчитали среднее относительное число заявок в системах сети. Нахождение ожидаемого дохода для предприятия, а так же решена оптимизационная задача.
По полученным в работе результатам можно сделать выводы:
1. В модели с разнотипными заявками в качестве периферийных систем выступают приемная и производственные отделы №1-5 предприятия, центральной системой является расчетно-сметовая отдел. В приемной и расчетно-сметовом отделе не различаются типы заявок. В периферийные системы различаются по типу заявки. В данной модели можно отметить, что ожидаемый доход приближен к реальному с осени по весну. Реальный доход в летний период снижается.
2. В третьей главе рассматривается задача оптимизации числа сотрудников на предприятии УП «Проектный институт Гродногипрозем».
Не нашли, что искали? Воспользуйтесь поиском: