
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ВЫПОЛНЕНИЕ КОМПЛЕКСНЫХ ЧЕРТЕЖЕЙ И АКСОНОМЕТРИЧЕСКИХ ИЗОБРАЖЕНИЙ ГЕОМЕТРИЧЕСКИХ ТЕЛ С НАХОЖДЕНИЕМ ПРОЕКЦИЙ ТОЧЕК НА ИХ ПОВЕРХНОСТЯХ
ЦЕЛЬ РАБОТЫ.
Научиться: 1) выполнять комплексные чертежи геометрических тел,
2) выполнять аксонометрические изображения геометрических тел,
3) находить проекций точек на поверхностях геометрических тел.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Аксонометрические проекции
Для получения аксонометрии детали располагаем ее внутри трехгранного угла, образованного плоскостями проекций Н, V и W (рис. 1 ). Деталь вместе с плоскостями проекций спроецируем на аксонометрическую плоскость проекций.
Виды аксонометрических проекций, расположение аксонометрических осей и коэффициенты искажения линейных размеров показаны на рис. 1
Аксонометрические проекции многоугольников строятся по координатам их вершин.
Аксонометрические проекции окружности получаются построением.
Построение окружности в изометрии
Для построения овала в плоскости Н проводят вертикальную и горизонтальную оси овала (рис. 2 ). Из точки пересечения осей О проводят вспомогательную окружность диаметром d, равным действительной величине диаметра изображаемой окружности, и находят точки n 1 n2, n3, na4 пересечении этой окружности с аксонометрическими осями х и у. Из точек т, и т2 пересечения вспомогательной окружности с осью z, как из
центров радиусом R=m1,n1 проводят две дуги 2 3 и I 4,
принадлежащие овалу. Пересечения этих дуг с осью z
дают точки С и D.
Из центра О радиусом ОС, равным половине малой оси овала, засекают на большой оси овала АВ точки О1 и 02. Точки /, 2, 3 и 4 сопряжений дуг радиусов R и R, находят, соединяя точки т, и т2 с точками 0; и 02 и продолжая прямые до пересечения с дугами 23 и 14. Из точек О1 и Ог радиусом R1=O1l проводят две дуги.
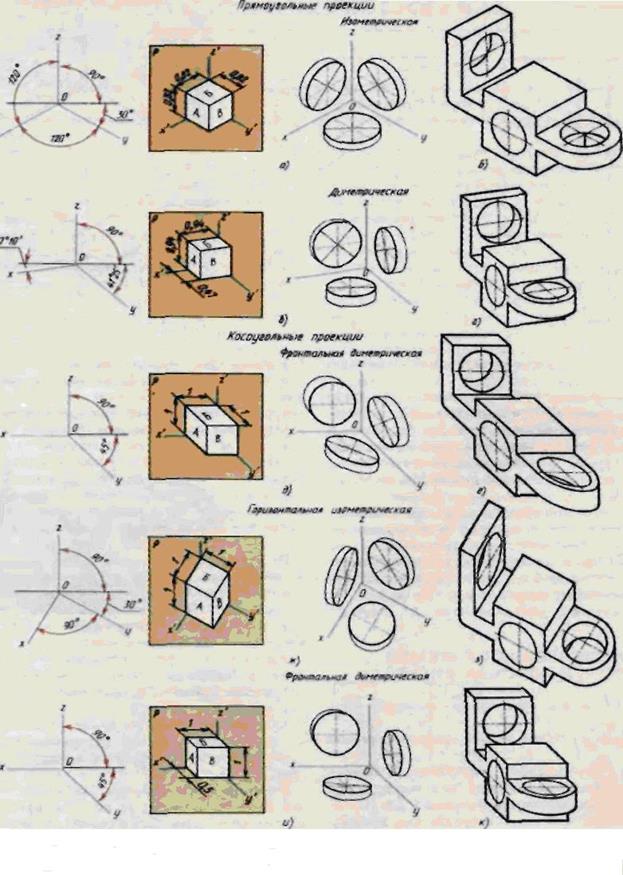
Рис.1

Рис.2
Чертежи геометрических тел.
Деталь любой формы можно представить как совокупность отдельных геометрических тел.
Для примера возьмем деталь (рис. 3а) и проанализируем ее форму.
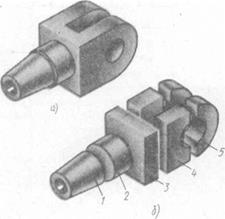
Рис.3
Мысленно расчленив ее на отдельные элементы, получим следующие геометрические тела (рис. 36): 1 — усеченный конус с отверстием в виде цилиндра; 2 — прямой круговой цилиндр; 3 — параллелепипед; 4 — два прямоугольных параллелепипеда с цилиндрическими отверстиями; 5 — два полых полуцилиндра. Для выполнения комплексных чертежей необходимо усвоить методы проецирования отдельных геометрических тел, а также точек и линий, расположенных на поверхности этих тел.
Для определения видимости поверхностей тел и точек на них воспользуемся схемой приведенной на рис.4.

Рис.4
Геометрические тела делятся на:
- многогранники - тела ограниченные плоскими многоугольниками (гранями). Многоугольники имеют: ребрами - пересечение граней; и вершины - углы, образованные пересечением ребер,
- тела вращения - поверхности, которые получаются в результате вращения какой-либо линии (образующей) вокруг неподвижной оси.
Проекция призмы
Построение проекций правильной прямой шестиугольной призмы (рис. 5) начинается с выполнения ее горизонтальной проекции — правильного шестиугольника. Из вершин этого шестиугольника проводят вертикальные линии связи и строят фронтальную проекцию нижнего основания призмы. Эта проекция изображается отрезком горизонтальной прямой. От этой прямой вверх откладывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчивают фронтальные проекции ребер — отрезки вертикальных прямых, равные высоте призмы. Фронтальные проекции передних и задних ребер совпадают. Горизонтальные проекции боковых граней изображаются в виде отрезков прямых. Передняя боковая грань 1243 изображается на плоскости V без искажения. а на плоскости W — в виде прямой линии. Фронтальные и профильные проекции остальных граней изображаются с искажением.
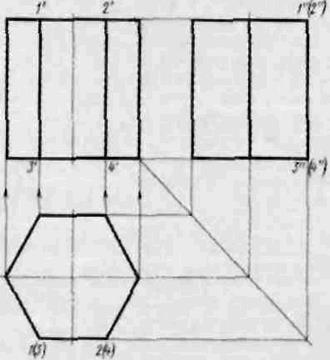
Рис.5
По имеющемуся комплексному чертежу призмы можно выполнить ее изометрическую проекцию по координатам вершин. Для этого вначале строят нижнее основание призмы, а затем вертикальные ребра и верхнее основание.
По координатам точки лежащей на поверхности призмы, взятым с комплексного чертежа, можно построить аксонометрическую проекцию этой точки.
ПРОЕКЦИИ ЦИЛИНДРА
Боковая поверхность прямого кругового цилиндра получается вращением отрезка образующей вокруг оси, параллельной этому отрезку.

|
Рис.6
Построение начинают с изображения основания цилиндра (рис.6а). Так как окружность расположена на плоскости Н, то она проецируется на эту плоскость без искажения. Фронтальная проекция окружности представляет собой отрезок горизонтальной прямой линии, равный диаметру окружности основания.
После построения основания на фронтальной проекции проводят две очерковые (крайние) образующие и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, который является фронтальной проекцией верхнего основания цилиндра.
Определение недостающих проекций точек А и В, расположенных на поверхности цилиндра, по заданным фронтальным проекциям в данном случае затруднений не вызывает, так как вся горизонтальная проекция боковой поверхности цилиндра представляет собой окружность. Следовательно, горизонтальные проекции точек А и В можно найти, проводя из их фронтальных проекций вертикальные линии связи до пересечения с окружностью в искомых точках а и 6.
Профильные проекции точек А и В строят также при помощи вертикальных и горизонтальных линий связи.
Изометрическую проекцию цилиндра вычерчивают, как показано на рис.6б.
В изометрии точки А и В строят по их координатам.
ПРОЕКЦИЯ ПИРАМИДЫ
Построение проекции пирамиды (рис.7) начинается с построения основания, горизонтальная проекция которого представляет собой многоугольник без искажения. Фронтальная проекция основания — отрезок горизонтальной прямой.

Рис.7
Из горизонтальной проекции точки s (вершины пирамиды) проводят вертикальную линию связи, на которой на фронтальной проекции от оси х откладывают высоту пирамиды и получают фронтальную проекцию s' вершины. Соединяя точку s' с точками 1', 2'и 3', получают фронтальные проекции ребер пирамиды.
Горизонтальные проекции ребер получают, соединяя горизонтальную проекцию точки S с горизонтальными проекциями точек 1, 2 и 3.
Для нахождения недостающих проекций точки А, расположенной на грани пирамиды 1 s2 ( фронтальная проекция а' задана) существуют два способа.
1 способ (рис.7а). Проведем через а' вспомогательную прямую любого направления и продолжим ее до пересечения с фронтальными проекциями 1's' и 2's ребер в точках n' и т'. Затем проведем из точек п' и т' линии связи до пересечения с горизонтальными проекциями n' и 2s этих ребер в точках n и m. Соединив n с т, получим горизонтальную проекцию вспомогательной прямой. на которой с помощью линии связи найдем искомую горизонтальную проекцию а точки А. Профильную проекцию этой точки находят по линиям связи.
2 способ (рис.7б). Через заданную фронтальную проекцию а' точки А проводят вспомогательную прямую, проходящую через вершину пирамиды и расположенную на се грани. Горизонтальную проекцию ns вспомогательной прямой находят, применяя линию связи. Искомая горизонтальная проекция а точки А находится на пересечении линии связи, проведенной из точки а', с горизонтальной проекцией ns вспомогательной прямой.
Аксонометрическую проекцию точки А, расположенной на грани пирамиды (рис.7в), строит по координатам, которые берут с комплексного чертежа.
ПРОЕКЦИИ КОНУСОВ
Боковая поверхность конуса получается при вращении отрезка BS вокруг оси конуса.
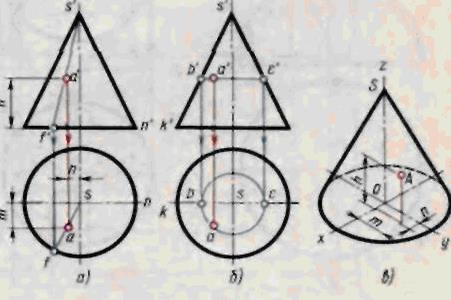
Рис.8
Последовательность построения проекций конуса аналогична цилиндру. Сначала строят две проекции основания. Горизонтальная проекция основания - окружность. Фронтальной проекцией будет горизонтальный отрезок, равный диаметру этой окружности. На фронтальной проекции из середины основания восставляют перпендикуляр и на нем откладывают высоту конуса. Полученную фронтальную проекцию вершины конусу соединяют прямыми с концами фронтальной проекции основания и получают фронтальную проекцию конуса.
Для нахождения недостающих проекций точки А, расположенной на боковой поверхности существуют два способа.
1 способ (рис.8а). Проводят фронтальную проекцию s'a'f вспомогательной образующей. Пользуясь вертикальной линией связи, проведенной из точки f, расположенной на фронтальной проекции окружности основания, находят горизонтальную проекцию s f этой образующей, на которой при помощи линии связи, проходящей через а', находят искомую точку а.
2 способ (рис.8б). Вспомогательной линией, проходящей через точку А, будет окружность, расположенная на конической поверхности и параллельная плоскости Н. Фронтальная проекция этой окружности изображается в виде отрезка b'с' горизонтальной прямой, величина которого равна диаметру вспомогательной окружности. Искомая горизонтальная проекция а точки А находится на пересечении линии связи, опущенной из точки о', с горизонтальной проекцией вспомогательной окружности.
Если заданная фронтальная проекция точки В расположена на контурной (очерковой) образующей SK, то горизонтальная проекция точки находится без вспомогательного построения.
Аксонометрическую проекцию точки А строит по координатам, которые берут с комплексного чертежа (рис.8в)
ЗАДАНИЕ
Боголюбов С.К., «Индивидуальные задания по курсу черчения». Задание 34, первый абзац (геометрические тела по отдельности)
1) По заданным размерам построить в трех проекциях геометрические тела,
2) Построить аксонометрические проекции геометрических тел,
3) найти проекций точек, расположенных на поверхностях геометрических тел.
Студенты по своему желанию могут сделать более сложное задание - Задание 34, второй абзац (группа геометрических тел).
Выполнение усложненного задания приветствуется и учитывается при оценивании работы. Если выполнены оба задания, ставятся две оценки.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1) Выполнить разметку листа, т.е. определить, с учетом габаритных размеров, место расположение всех изображений.
2) Начертить комплексные чертежи геометрических тел.
3) Начертить аксонометрические изображения геометрических тел.
4) По желанию найти проекций точек, заданных в задании, на поверхностях геометрических тел.
5) Найти проекций точек, заданных преподавателем, на поверхностях геометрических тел.
ПЕРЕЧЕНЬ ОБЪЕКТОВ КОНТРОЛЯ И ОЦЕНКИ
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| Умение решать графические задачи | - Прямоугольное проецирование цилиндра, конуса, призмы, пирамиды - Построение аксонометрических проекций геометрических тел | 100 баллов |
| Знание способов графического представления пространственных образов | - Классификация видов проецирования - Описание системы координат и плоскостей проекций прямоугольного проецирования пространственных объектов - Воспроизведение способов построения комплексных чертежей геометрических тел - Классификация видов аксонометрических проекций по ГОСТ 2.317-69 - Изложение порядка построения аксонометрических проекций геометрических тел |
Исходная оценка – 100 баллов.
За небольшие ошибки и неточности в графической работе снимается от 1 до 5 баллов.
За существенные ошибки, нарушение стандартов снимается от 10 до 20 баллов.
За высокое графическое качество выполнения работы может быть добавлено, а за низкое снято до 10 баллов.
За хорошее знание и понимание теоретических понятий по теме работы может быть добавлено до 10 баллов, а за плохое снято до 20 баллов.
За степень самостоятельности проявленные при выполнении работы добавляется или снимается до 20 баллов.
За выполнение работы повышенной сложности добавляется до 20 баллов.
Шкала оценки
| Количество набранных баллов | Оценка графической работы | |
| балл (отметка) | вербальный аналог | |
| Свыше 90 | отлично | |
| От 80 до 89 | хорошо | |
| От 60 до 79 | удовлетворительно | |
| менее 60 | неудовлетворительно |
КОНТРОЛЬНЫЕ ВОПРОСЫ:
10. Какие бывают виды аксонометрических проекций?
11. Как располагаются координатные оси в различных видах аксонометрических проекций?
12. Какой коэффициент искажения по осям в диметрии?
13. Как определяют проекции точек, лежащих на поверхности объемных фигур?
ЛИТЕРАТУРА
1. Березина Н.А. Инженерная графика — M.: Инфра-М, 2010
2. Чекмарев А.А. Инженерная графика — M.: Инфра-М, 2009
3. Боголюбов C.K. Инженерная графика — M.: Машиностроение, 2006
4. Боголюбов С.Н. Задания по курсу черчения: учебник для СПО.- М.: Высшая школа, 2007
5. Боголюбов С.K. Индивидуальные задания по курсу черчения — M.: Высшaя школа, 1992
Не нашли, что искали? Воспользуйтесь поиском: