ПОСТРОЕНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА, АКСОНОМЕТРИИ И РАЗВЕРТКИ ПОВЕРХНОСТИ УСЕЧЕННОГО ГЕОМЕТРИЧЕСКОГО ТЕЛА

ЦЕЛЬ РАБОТЫ.

Научиться: 1) вычерчивать комплексный чертеж и аксонометрию усеченного геометрического тела,

2) находить натуральную величину элементов усеченного геометрического тела и выполнять развертку его поверхности.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Детали очень часто имеют формы, представляющие собой различные геометрические поверхности, рассеченные плоскостями.

Пример таких деталей сечения приведен на рис. 1. Пирамида, конус и цилиндр рассечены фронтально проецирующей плоскостью.

Рис.1

СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ

Для полых деталей изготовленных из листа часто, кроме чертежа необходимо выполнить развертку их поверхности (раскрой). Обычно это применяется при изготовлении обшивки летательных аппаратов, корпусов блоков радиоаппаратуры, кожухов для закрывания механизмов, частей трубопроводов и вентиляционных устройств, и т. д.

При выполнении разверток поверхностей геометрических тел требуется определить действительную величину элементов тел, которые на чертеже изображаются в искаженном виде. Для этого применяются особые способы построения, цель которых получить новую проекцию элемента детали, представляющую собой его действительную величину или вид.

Такими способами являются: способ перемены плоскостей проекций, способ совмещения и способ вращения.

СПОСОБ ПЕРЕМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Сущность способа перемены плоскостей проекций заключается в том, что вводится новая плоскостей проекций, на которую проецируются заданная фигура. При этом фигура не меняют своего положения в пространстве. Новая плоскость перпендикулярна одной из основных плоскостей и параллельна заданной фигуре. (Рис.2)

Рис.2

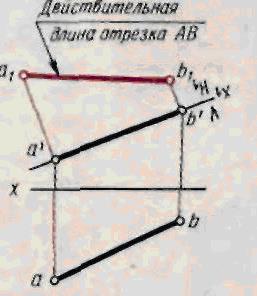
Рис.3

Определим способом перемены плоскостей проекций действительную длину отрезка АВ (рис. 3). В этом случае новая плоскость проекций должна быть выбрана так, чтобы она была параллельна отрезку АВ.

Заменим плоскость Н новой горизонтальной плоскостью проекций Н₁ (рис.3).

Новую ось проекций х₁, проведем (для упрощения построений) через фронтальную проекцию отрезка а₁'Ь₁'. Координату у_л откладываем на перпендикуляре к новой оси.x₁ отточки а'. а координату у в — от точки b '.
Отложив эти координаты, получаем новые горизонтальные проекции а₁, и b₁ точек А и В. Соединив точки а₁ и b₁ на новой горизонтальной плоскости проекцийH₁ получим действительную длину отрезка АВ.

Подобными приемами построений можно определить действительный вид многоугольники 12345, плоскость которого является фронтально-проецирующей (рис. 4).

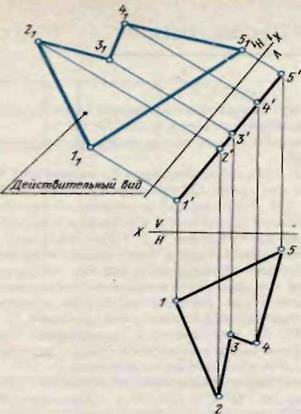
Рис.4

В этом случае требуется заменить Н на Н₁. ось проекций которой проводится параллельно фронтальной проекции многоугольника на произвольном расстоянии.

Для нахождения, например, новой горизонтальной проекции точки 3 из точки 3' восставляют перпендикуляр и от оси х₁ откладываем на этом перпендикуляре расстояние, равное расстоянию от точки 3 до оси х. Точка 3₁ будет новой горизонтальной проекцией точки 3. Так же находят все точки. Затем, соединив их прямыми линиями, получают действительный вид многоугольника.

СПОСОБ СОВМЕЩЕНИЯ

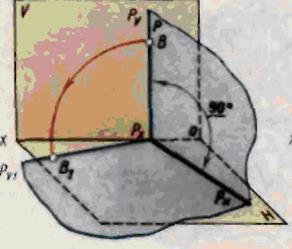
Сущность способа совмещении заключается в том, что плоскость, заданную следами, вращают вокруг одного из следов этой плоскости до совмещения с соответствующей плоскостью проекций, например, вокруг следа Р„ до совмещения с горизонтальной плоскостью проекций (рис. 5а ). Изображения отрезка прямой или плоской фигуры, лежащей в заданной плоскости Р, получаются без искажения.

а)

б)

Рис.5

Определения действительной длины отрезка прямой АВ способом совмещения решается следующим путем (рис. 5б).

Задается фронтально-проецирующая плоскость Р. Фронтальный след P_v проводят через точки а' и b.' Горизонтальный след Р_н. проводят перпендикулярно оси X через точку а, расположенную на плоскости Н. Плоскость Р совмещают с плоскостью Н. совмещенное положение следа P_v совпадает с осью х. Из точки Р_х радиусом Р_х b' делают засечку дугой окружности на совмещенном следе Р_v1, и из точки пересечения восставляют перпендикуляр к оси х. Из точки b опускают перпендикуляр на след R_н и, продолжая его до пересечения с прямой, перпендикулярной к оси х, получают совмещенное положение точки В — точку by Соединив точки а'₁ и b ₁' находят совмещенное положение отрезка АВ. Которое и будет его действительной длиной.

СПОСОБ ВРАЩЕНИЯ

Сущность способа вращения заключается в том, что заданные точка, линия или плоская фигура вращаются вокруг оси, перпендикулярной к одной из плоскостей проекций, до требуемого положения параллельного относительно какой-либо плоскости проекций. Если вращается фигура или тело, то каждая их точка будет перемещаться по окружности. Таким образом, при вращении точки вокруг оси, перпендикулярной к какой-либо плоскости проекций, проекция точки на эту плоскость перемещается по окружности, а вторая проекция — по прямой, параллельной оси проекций.(рис.6)

Рис.6

Вращение отрезка прямой вокруг оси, перпендикулярной к плоскости проекций, можно рассматривать как вращение двух точек этого отрезка.

Построения на комплексном чертеже упрощаются если ось вращения провести через какую-либо конечную точку вращаемого отрезка прямой. В этом случае достаточно повернуть только одну точку отрезка, так как другая точка, расположенная на оси вращения остается неподвижной.

Допустим требуется определить способом вращения действительную длину отрезка общего положения АВ (рис. 6 а).

Через конец отрезка А (рис. 6 б) проводят ось вращения MN перпендикулярно плоскости Н. Относительно этой оси вращается второй конец отрезка — точка В. Чтобы получить на комплексном чертеже действительную длину отрезка, надо повернуть его так, чтобы он был параллелен плоскости V.

После вращения горизонтальная проекция отрезка должна быть параллельна оси х, поэтому на этой плоскости проекций и начинается построение. Из точки а радиусом ab описывают дугу окружности до пересечения с прямой, проведенной из точки а параллельно оси х. Точка пересечения b₁, — новая горизонтальная проекция точки В. Фронтальную проекцию точки В находят, проводя вертикальную линию связи из точки b ₁, до пересечения с прямой, проведенной из точки b ' параллельно оси х (в данном случае эта прямая совпадает с осью х). Соединив точки b'₁ и а', на плоскости V получают действительную длину отрезка А В.

Эту задачу можно решить вращением отрезка АВ относительно оси, перпендикулярной к плоскости V.(рис.6в)

Построение комплексного чертежа, аксонометрии и развертки поверхности усеченного геометрического тела рассмотрим на примере цилиндра и пирамиды.

Не нашли, что искали? Воспользуйтесь поиском: