3 страница

Заттың меншікті жылусыйымдылығы С -1кг затты 1К-ге қыздырғандағы кеткен жылу мөлшеріне тең шама. Өлшем бірлігі- Дж/кг*К. C=δQ/mdT.

Билет

1.Электростатикалық өріс. Кулон заңы және ортаның электр өтімділігі.

Электр өрісі-электр зарядтары өзара ісерлесетін материяның түрі. Электр өрісін заряд туғызады. Қозғалмайтын заряд өрісін-электростатикалық деп атайды. Электр өрісін өлшеуіш құралдармен байқауға болады. Кулон заңы: нүктелік екі зарядтың өзара әсер күші әрбір зарядтардың шамаларына пропорционал және олардың арақашықтығының квадратына кері пропорционал.Формуласы:

. k-пропорционалдық коэффициен, q₁ мен q₂ өзара әсерлесетін зарядтардың шамалары, r-олардың арақашықтығы. Өлшем бірлігі:Кулон(K). Егер әсерлесуші зарядтар изотропты ортада болса, онда кулон күші мынаған тең: ; Мұндағы ε-ортаның диэлектрлік өтімділігі. ε=1.

2 Фотоэффект.Эйнштейн теңдеуі.Фотоэффекттің заңдары.

Фотоэффект деп түскен жарық әсерінен заттан электрондардың бөлініп шығу құбылысын айтады. Фотоэффектің үш түрі бар: ішкі, вентильді және сыртқы. Шалаөткізгіштер н/е диэлектриктердің ішінде байланыстағы электрондардың жарық әсерінен сыртқа шықпай бос электрондарға айналу құбылысы ішкі фотоэффект д.а. Екі түрлі шала өткізгіштіктердің н/е шалаөткізгіш пен металл беттері түйіскен жерге жарық түскенде электр қозғаушы күшінің пайда болуы вентильдік фотоэффект д.а. Жарық әсерінен заттан электрондардың босап шығуы сыртқы фотоэффект д.а. Сыртқы фотоэффектке арналған Эйнштейн теңдеуі: hv=A+ . 1заң:Столетов заңы: түскен жарықтың жиілігінің бекітілген мәнінде бірлік уақыт ішінде фотокатодтан шыққан фотоэлектрондар саны жарық интенсивтілігіне пропорционал. 2заң:фотоэлектрондардың бастапқы максимал жылдамдықтары түскен жарықтың интенсивтілігіне тәуелді емес, тек жарықтың υ жиілігімен анықталады. 3заң:әр зат үшін фотоэффектің қызыл шекарасы бар-одан төмен мәнде фотоэффект мүмкін болмайтын жарық жиілігінің минимал мәні υ₀ (заттың химиялық құрылымына және зат бетінің күйіне байланысты).

Билет

1.Сызықтық және бұрыштық үдеулердің арасындағы байланыс.

Механикада бұрылу бұрышын радианмен өлшеу келісілген. Радиан — ɭ доғасының щындығы R радиусына тең болатын φ центрлік бұрыш. Бұрылу бұрышының уақыт өтуімен өзгеруін бұрыштық жылдамдық арқылы сипаттайды.

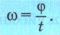
Бұрыштық жылдамдық деп дененің бұрылу бұрышының осы бұрылуға кеткен уақытқа қатынасымен өлшенетін шаманы айтады. Бұрылу бұрышы φ әрпімен белгіленеді.

Дененің шеңбер бойымен қозғалысын қарастырғанда, дененің түзусызықты қозғалысын сипаттайтын жылдамдық та колданыла береді. Бірақ дененің шеңбер бойымен қозғалысыжағдайында оны сызықтық жылдамдық деп атау келісілген.

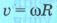
Бұрыштық жылдамдық пен сызықтық жылдамдықтың жоғарыда алынған формулалары есеп шығару кезінде жиі колданылады.

2.Магнит өрісінің энергиясы.

Тізбектегі н/е контурдағы ток күшейгенде оның туғызатын магнит өрісі де күшейеді, сондықтан осы магнит өрісінен өнген энергияы магнит өрісінің энергиясы болып табылады. Формуласы: . Магнит өрісінің энергиясының тығыздығы: .

Билет

1.Магнит өрісінің қозғалыстағы зарядқа әсері.Лоренц күші. Магнит өрісі тек тогы бар өткізгішке ғана емес, сол сияқты кез-келген қозғалыстағы зарядтарғада әсер ететіндігін көптеген эксперименттердің нәтижелері дәлелдеді. Ал магнит өрісіндегі әр зарядқа әсер ететін күшті Лоренц күші деп атайды. Лоренц күшінің өрнегі: F_Л=EυBsinα. Мұндағы υ-электрондардың бағытталған жылдамдығы, α-магнит өрісінің күш сызықтарымен электрондардың бағытталған жылдамдығының арасындағы бұрыш. Лоренц күшінің бағытн сол қол ережесі б/ша анықтайды, яғни магнит индукциясы алақанды тесіп өтсе, саусақтар электрондар жылдамдығының бағытын көрсетсе, онда бас бармақ Лоренц күшінің бағытын анықтайды. Жалпы магнит өрісіндегі қозғалыстағы зарядқа магнит индукциясынан басқа, кернеулігі Ē электр өрісіде әсер етеді. Олай болса, зарядқа әсер етуші қорытқы күш электрлік күш пен Лоренц күшінің қосындысына тең болады. Егер F_k=eĒ және F_Л=EυB екендігін ескерсек, онда қорытқы күш мынаған тең F_Л=eĒ+e[υB] болады. Бұл өрнек Лоренц формуласы деп аталады.

2.Шредингердің стационар теңдеуі.Еркін бөлшектің қозғалысы. Шредингердің ортақ теңдеуінің негізгі жеке жағдайы Ψ-дің уақытқы тәуелдігін шығаратын стационар күйлер үшін Шредингер теңдеуі болып табылады, сондықтан бұл күйлері энергия мәні орнықты болады. Бұл жағдайдағы бөлшек қозғалатын күш өрісі стационарлы, яғни U=U_(x,y,z) көрініп тұрғандай, уақытқа тәуелді болмайды және потенциалдық энергияның мәніне ие болады. Теңдеудің шешімі екі функцияның туындысы түрінде көрсетілуі мүмкін-тек координат функциясы және тек уақыт функциясы: Ψ(x,y,z,t)=Ψ(x,y,z)exp(-i , мүндағы Е-бөлшектің толық энергиясы. Шредингердің теңдеуі: - Қысқартылудан кейін мына түрге ие болады: н/е ∆Ψ+ 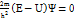-стационар күй үшін Шредингер теңдеуі.

Еркін бөлшектер үшін U(x)=0(X осінің бойымен қозғалысын делік). Шредингердің теңдеуінің шешімінен 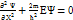. Ψ(x,t)= Aexp(-iwt+ikx)=Aexp(- ) функциясы болады. Мұндағы A=const, k= толоқындық сан, ол кез-келген оң мәнді қабылдай алады. E= -энергияның үздіксіз спектрі. Сондықтан еркін кванттық бөлшек де-Бройльдің жазық монохроматты толқынымен сипатталады. Бұған уақытқа тәуелді емес кеңістіктегі берілген нүктедегі бөлшектердің табу ықтималдығы сәкес келеді: |Ψ|²=ΨΨ^*=|A|², яғни кеңістіктегі еркін бөлшектің барлық жағдайы тең ықтималды болып табылады.

Билет

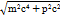1.Де-Бройль толқындары және оның қасиеттері. Массасы m,υ жылдамдығымен еркін қозғалатын бөлшеті қарастырайық. Де-Бройль толқынының фазалық жылдамдығы: яғни де-Бройль толқынының фазалық эылдамдығы(c> ). E=h , P=hk, k= -толқындық сан, арақатынастарды қолданылған. Де-Бройль толқынының топ жылдамдығы: u= = . Еркін бөлшек үшін: E= ,сондықтан u= = = . Де-Бройль толқынының топ жылдамдығы бөлшектің жылдамдығына тең. Басқа сөзбен айтқанда, де-Бройль толқындары бөлшектермен бірге орналасады. Фотон үшін: = 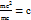және u= .

2.Қатты денелердің деформациясы.Гук заңы. Серпімді және серпімсіз деформация.

Қатты денелердің сыртқы күштің әсерінен пішінімен өлшемін өзгертуін деформация деп атайды. Серіппенің деформациядан кейінгі ұзаруын ∆ , деформацияға дейінгі ұзындығына бөлсек, дененің салыстырмалы деформациясы шығады:ε= . н/е салыстырмалы деформация кернеуге тура пропорционал ε=ασ. Материалдың серпімді қасиеттерін қарастырғанда деген шама қолданылады, бұл серпімді модулі н/е Юнг модулі д.а. Юнг модулін қолданып салыстырмалы деформацияны мына түрде жазуға болады: ε= . Мұндағы α- материалдың табиғатына б/сты пропорционалдық коэффициенті, ол Пуассон коэффициенті д.а. Юнг модулінің өлшем бірлігі-Па. Енді теңдеуді теңестіре отырып, былай жазуға болады: ε= = бұдан F= бұл Гук заңы болып табылады. Бұдан серпімді деформация кезінде серіппенің ұзаруы әсер етуші күшке тура пропорционал екендігі шығады, мұндағы к-пропорционалдық коэффициент н/е серпімділік коэфц д.а.

Гук заңы — тегеурін мен одан туған пішін өзгерісі арасындағы тура пропорционалдықты анықтайтын заң.

Билет

1.Жарықтың толқындық сипаттамалары.Гюйгенс принципі.

Жарықтың толқындық теориясы Гюйгенс принципіне негізднлген. Ол былай тұжырымдалады: толқын таралғанда жететін нүкте келесі толқындардың көзі болады. Ал осы толқындардың таралғанда пайда болатын беті толқындық фронт д.а. Гюйгенс принципін пайдалана отырып, жарықтың шағылу және сыну заңдары қорытып шығаруға болады, айталық, екі ортаның бөліну шекарасына I бойымен бағытталған жазық толқын түссін (АВ-жазық толқын). (t-yақытында) жарық фронты ВС- қашықтығын жүрсе, екінші ретті толқындардың фронты А нүктесінен АD қашықтығын жүреді. Жарық шағылғанда: ∆ABC=∆ADC сәйкесінше i₁^,=i₁ Жарық сынғанда: t-уақытында түскен толқынның BC= фронты жол жүреді, ал сынған толқынның фронты-AD= 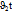. AC=BC/sini₁=AD/sini₂ қатынасынан келесі қатынастар шығады: .

2.Кинетикалық және потенциалдық энергия. Энергияның сақталу заңы.

Материалдық нүктеге түсірілген күштің жасаған жұмысы дененің жылдамдығының өзгеруіне байланысты бұл бай/с материалдық нүктенің кинетикалық энергиясы д.а. Егер дене инерция күшінің нәтижесінде ds -ке орналастырса, істелген жұмыс dA=Fds, бұдан: dA=Fds=mads=m яғни v жылдамдықпен қозғалатын массасы m дененің кинетикалық энергиясы: dE_k= Сонымен кинет энерг дененің тек массасы мен жылдамдығына тәуелді. Сондықтан, ол, 1жүйенің күй функциясы болып табылады; 2 барлық уақытта оң; 3 әр түрлі инерциалды санақ жүйесінде бірдей емес. Потенциалдық энергия-денелердің өзара орналасуын және араларындағы әсерлесу күшін сипаттайтын жүйенің механикалық энергиясы. Потенц энерг денелердің н/е олардың бөлщектерінің өзара орналасуы кезіндегі жұмыс қорымен өлшенеді. dA=mgdh н/е A=E_p=mgh E_p= x-ұзындыққа созылған серіппенің потец энергиясы. Энергия жоғалмайды ж/е жоқтан пайда болмайды, ол тек бір түрден екінші түрге ғана ауысады. Энергияның бір түрі қаншаға кемісе, екінші түрі соншаға артады. Басқаша айтқанда, қозғалыссыз материя болмайды. Қозғалыс-материяның өмір сүру формасы. Дененің қозғалыс кезінде, кез-келген уақыт мезетінде оның кинет/қ ж/е потенц энергияның қосындысы тұрақты болады: E_k+E_p=const.

Билет

1.Қатты дененің айналмалы қозғалысының динамикасы.Күш моменті. Инерция моменті.

Айналмалы қозғалыстағы қатты дененің кинетикалық энергиясы 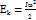егер дене әрі ілгерлемелі әрі айналмалы қозғалыста болса онда толық кинетикалық энергия

Массасы m дененің А нүктесінде қозғалысын қарастырғанда әсе етуші F күштің O нүктесінен күш бағытына түсірілген rcosα перпендикуляр ұзындығының көбейтіндісіне тен шаманы О нүктесіне қатысты күш моменті болып табылады. M=Frcosα мұндағы rcosα=l күш иіні деп аталады. Яғни күш пен иінің көбейтіндісі күш млменті деп аталады. M=Fl өлшем бірлігі (Н*м).

Дененің массасымен оның айналу центрінең денеге дейінгі арақашықтығының квадратының көбейтіндісіне тең шаманы инерция моменті деп атайды. J=mr²

2.Ядро құрылысы.Масса ақауы.

1833 ж. Роберт Броун өсімдік материалынан жасушалық ядроны ашқан. Ол микроскоп арқылы тозаң жіпшелерінің жасушаларын қарап, дөңгеленген формалы денешіктерді тапқан. Оны "nuclei" — ядро деп атаған. Ядро жасушаның ортасында орналасқан дөңгелек немесе сопақша формалы жасушаның ең ірі органоиді. Ядро үш бөліктен тұрады: ортасында орналасқан —ядрошықтан, ядроның сұйық бөлігі — нуклеоплазмадан және ядролық мембранадан.Ядроның байланыс энергиясы дегеніміз - ядроны түгелімен жеке нуклондарға ыдырату үшін қажет энергияны айтамыз.
Энергияның сақталу заңына сәйкес, жеке бөлшектерден ядро түзілгенде бөлініп шығатын энергия мен байланыс энергиясы өзара тең.
Кез келген ядроның байланыс энергиясын оның массасын дәл өлшеу арқылы анықтауға болады.
Эйнштейннің Е=тс2 қатынасын пайдалана отырып, байланыс энергиясын есептеуі е болады.

Нуклондардың ядродағы байланыс энергиясы.

Мя< Z*mp + N*mn

∆М= Z*mp + N*mn - Mя — масса ақауының формуласы;

Массалар ақауы деп – жеке бөлшектер массаларының қосындысынан сол бөлшектерден құралған ядро массасын алып тастағандағы қалған ∆М қалдық массаны айтамыз

Еб= ΔM*c2=(Z*mp + N*mn - Mя)*c2 немесе Еб=(Z*mН + N*mn – Mа)*c2;

Атом ядросын түгелімен жеке нуклонға ыдырату үшін қажетті минимал энергияны-ядроның байланыс энергиясы дейміз.

Энергия үшін МэВ қолданылады:

Еб= (Z*mp + N*mn - Mя)*931,5 МэВ немесе Еб=(Z*mН + N*mn – Mа)*931,5 МэВ.

∆М= Еб / c2.

Байланыс энергиясы өте ғаламат. Екі вагон тас көмірді жаққан кезде қанша энергия мөлшері бөлінсе, сутегінен 4 г гелий массасын түзу үшін сондай энергия бөлінеді. Барлық үлкен Әлем кеңістігінде, оның ішінде жер шарында, сутегі — ең көп таралған элементтердің бірі. Сондықтан физиктердің, барлық басқа мамандардың негізгі мақсаты сутегі энергиясын бейбіт мақсат үшін қолдану.

Масса ақауы, масса дефектісі — атом ядросын құраушы нуклондар (нейтрондар мен протондар) массаларының қосындысы мен ядро массасының (М) арасындағы айырым ():=ZMp+(A––Z)Mn–M, мұндағы Z — ядродағы протондардың саны, А — ядроның массалық саны, Мр мен Мn — протон мен нейтронның массалары. М. а. массаның атомдық бірлігімен өрнектеледі және ол ядродағы нуклондардың байланыс энергиясына тең (кері таңбамен алынған). М. а. неғұрлым үлкен болса, соғұрлым байланыс энергиясы жоғары және ядро орнықты болады.

Билет

1.Радиоактивтілік және оның заңдары.

Радиоактивтілік (лат. radіo – сәуле шығару, actіvus – әсерлік) – орнықсыз атом ядроларының басқа элементтер ядросына бөлшектер немесе гамма-кванттар шығару арқылы өздігінен түрлену құбылысы. Радиоактивті ыдырау заңы — атом ядроларының әр түрлі бөлшектер мен сәулелер шығара отырып, өздігінен түрлену заңы.^[1][2] Радиоактивті ыдырау заңын Резерфорд ашқан:

немесе Эксперименттік зерттеулер радиоактивті ыдырау толығымен статистикалық заңдылыққа бағынатынын дәлелдеді. Белгілі бір радиоактивті изотоптың ядролары бірдей болады. Атом ядросының және ядролардың қайсысының ыдырайтыны - кездейсоқ оқиға. Мысал үшін, бір нуклидтің бірдей екі ядросын алайық. Ядроның біреуі 3 млрд жыл бұрын жұлдыздың қопарылысы кезінде, ал екінші ядро ядролық реакторда 3 мин бұрын пайда болсын. Ядролардың пайда болу уақытына қарамастан, келесі бір уақыт мезетінде екеуінің де ыдырауының ықтималдығы бірдей. Статистикалық құбылыстарды сипаттау үшін оқиғаның ықтималдығы ұғымын қолданады. Радиоактивті ядролар санының жартысы ыдырайтын уақыт аралығын жартылай ыдырау периоды 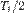деп атайды. Демек, радиоактивті ядролардық алғашкы саны болса, уақыт өткеннен кейін олардың саны болады. (8.11) өрнектен аламыз.Осы тендеуді логарифмдесек, , бұдан шығатыны . Ал 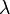тұрақты шама болғандықтан, жартылай ыдырау периоды тұрақты. Радиоактивті ыдырау заңын 1902 жылы Э.Резерфордпен Ф.Содди ашқан. Есептеулер радиоактивті ядроның орташа өмір сүру уақытын өрнегі арқылы анықтауға болатынын көрсетті. Ядроның орташа өмір сүру уақыты жартылай ыдырау периодына пропорционал. Радиоактивті ядроның ыдырау қасиетін сипаттайтын тағы бір шаманы айтуға болады. Уақыт бірлігі ішінде ыдырайтын ядролар санымен анықталатын шаманы радиоактивті заттың активтілігі () деп атайды: Активтіліктің Халықаралық жүйедегі () өлшем бірлігі — беккерель. 1 беккерель (Бк) — уақыт бірлігі 1 с ішінде бір ыдырау болатын радиоактивті препараттың активтілігі: 1 Бк = 1 ыдырау / 1 c. Іс жүзінде қолданылатын активтіліктің басқа да өлшем бірлігі бар, ол — кюри (Ки):1 Ки = 3,7 · 1010Бк; 1 мКи = 3,7 · 10⁷Бк.

2.Фотоэффект құбылысы.Сыртқы фотоэффект үшін Эйнштейн теңдеуі.

1887 неміс физигі Генрих Герц электр ұшқындары пайда болатын вибратор саңылауына ультра күлгін сәулелерін түсіргенде электр ұшқындары көбейіп, электр разрядының, күшейетіндігін байқаған. Одан кейін ғалымдар мырыш пластинкасына ультра күлгін сәуле түсіргенде одан теріс зарядтар ұшып шығып, мырыштың оң зарядталатындығын анықтаған.
Осы тәжірибелер металл пластинкаға жарық түскенде, одан электрондар ұшып шығатындығын көрсетеді. Осындай жарықтың әсерінен металл пластинкадан электрондардың ұшып шығу құбылысын фотоэффект құбылысы деп атаған.
Бұл фотоэффект құбылысын тереңірек зерттеген орыс физигі Столетов болды, Тәжiрибенiң негiзiнде фотоэффекттiң мынадай қарапайым үш заңы анықталды: 1. Фотоэлектрондардың максимальдi жылдамдығы түсiп тұрған жарықтың қарқындылығынан емес, оның жиiлiгiнен тәуелдi болады 2. Әрбiр затқа түсiп тұрған жарықтың жиiлiгi фотоэффекттiң қызыл шекарасы деп аталатын қандай да бiр νmin жиiлiгiнен кем болса фотоэффект құбылысы байқалмайды 3. Фотоэффект кезiнде уақыт бiрлiгiнде ұшып шығатын электрондардың саны (басқа сөзбен айтқанда тiзбектегi қанығу фототогының мәнi) түсетiн жарық қарқындылығына тура пропорционал.

Фотоэффект заңдарының теориялық түсiнiгiн 1905 жылы А.Эйнштейн бердi. Ол өз зерттеулерiнде М.Планктың кванттар жөнiндегi ұғымын одан әрi дамыта отырып, жарық тек кванттар түрiнде шығарылып ғана қоймайды, сонымен қатар кванттар түрiнде жұтылады да деп есептедi. Бұл жарық кванттарын ол фотондар деп атады. Эйнштейннiң бұл идеялары осы кезге дейiн үстемдiк етiп келген жарықтың толқындық теориясынан өзгеше, соны көзқарас едi. Бұл жерде жарықтың таралуы үздiксiз толқындық үрдiс ретiнде емес, ерекше жарық бөлшектерi – фотондардың с - ға тең жылдамдықпен қозғалатын ағыны ретiнде қарастырылады. Бұл тұрғыдан қарағанда, мәселен монохроматты жарыққа энергияларының мәндерi бiрдей, әрi hν-ге тең болатын фотондар сәйкес қойылады. Ал жарықтың затқа жұтылуы сәйкес фотондар осы затқа түскен кезде өз энергиясын түгелiмен заттың атомдары мен молекулаларына беруiмен түсiндiрiледi. Жарықтың табиғатына деген осы кванттық көзқарас фотоэффект құбылысының тәжiрибеден байқалатын барлық заңдылықтарын түсiндiруге мүмкiндiк бердi. мәселен, электрон металлдан ұшып шығуы үшiн металл-вакуум шекарасындағы потенциалдық тосқауылдан өтуi, яғни қандай да бiр A_шығ-ға тең шығу жұмысын iстеуi қажет. Бұған қажет энергияны электрон өзi жұтқан фотоннан алады. Фотон металл атомына жұтылған кезде өзiнiң ε_ν=hν -ға тең энергиясын толығымен электронға бередi. Онда мұндай фотоэлектрондар үшiн энергияның сақталу заңын мына түрде жазуға болады

Не нашли, что искали? Воспользуйтесь поиском: