5 страница. Малюс Заңы — өткен сызықты поляризацияланған жарық қарқындылығының cos α-ге пропорционал

Малюс Заңы — өткен сызықты поляризацияланған жарық қарқындылығының cos α-ге пропорционал азаятындығын өрнектейтін заң; мұндағы α — жарық поляризациясы жазықтығы мен прибор (анализатор) арасындағы бұрыш. Бұл заңды 1810 жылы француз физигі Э.Л.Малюс (1775 — 1812) ашқан. Егер І0 және І — анализаторға түсетін және одан шығатын жарық қарқындылықтарын сипаттаса, онда Малюс Заңы бойынша: І=І0cos2α түрінде орындалады. Өзгеше (сызықты емес) поляризацияланған жарықты екі сызықты поляризацияланған құраушылардың қосындысы түрінде қарастыруға болады. Олардың әрқайсысы үшін Малюс Заңы орындалады. Барлық поляризациялық приборлардан өтетін жарық қарқындылығы Малюс Заңы бойынша есептеледі, ал Малюс Заңы ескермейтін, α-ға тәуелді болатын шағылу кезіндегі шығындар басқа тәсілмен қосымша анықталады.

Билет

1.Айналмалы қозғалыс және оны сипаттайтын шамалар.

Қозғалыс кезінде дененің барлық нүктелері шеңберлер сызатын және олардың центрлері айналыс осі деп аталатын бір түзудің бойында жататын қозғалысты айналмалы қозғалыс деп атайды. Айналмалы қозғалысты қарастырғанда бұрыштық жылдамдық және бұрыштық үдеу ұғымдарын енгіземіз. Материалдық нүкте радиусы 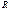шеңбер бойымен қозғалып, 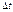уақыт мезетінде 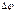бұрышына бұрылсын. Бұрыштық жылдамдық 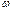деп, дененің бұрылу бұрышынан уақыт бойынша алынған бірінші ретті туындысына тең физикалық векторлық шаманы айтады.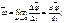 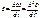болады, яғни айналмалы қозғалыстың бұрыштық үдеуі бұрыштық жылдамдықтан уақыт бойынша алынған бірінші ретті,ал бұрылу бұрышының екінші ретті туындысына тең болады. Бұрыштық үдеу векторлық шама оның бағыты бұрыштық үдеудің бағытымен бағыттас, өлшем бірлігі 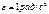болады. Егер қозғалыс үдемелі болса, 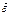векторы мен 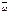векторы бағыттас болады, егер кемімелі болса 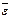векторы мен 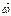қарама-қарсы бағытта болады.

Материалдық нүктенің ілгерімелі және айналмалы қозғалыстарын сипаттайтын шамалар өзара мынадай қатынаста болады:

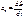, бұдан 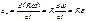немесе

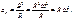немесе.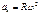

Айналмалы бірқалыпсыз қозғалыс кезіндегі қозғалыс теңдеулері:

,

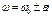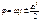
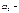бастапқы бұрыштық үдеу.

2.Тұрақты қысымдағы және тұрақты көлемдегі жылу сиымдылықтар.Майер теңдеуі.

Жылусыйымдылықтың зат мөлшеріне қатынасын меншікті жылусыйымдылық деп атайды. Меншікті жылусыйымдылықтың мынадай түрлері бар:

.

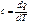массалық 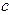, Дж/(кг×К); көлемдік 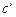, Дж/(м³×К); молдік 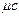, Дж/(кмоль×К). Идеал газдың жылусыйымдылығы температурадан тәуелді. Бұл белгілері бойынша нақтылы және орташа жылусыйымдылықтар болып ажыратылады. Температураның шексіз аз өзгеруіне сәйкес келетін жылусыйымдылықты нақты жылусыйымдылық деп

Температраның t₁-ден t₂-ге өзгеруіне сәйкес жылусыйымдылықты орташа жылусыйымдылық 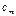деп атайды.

,

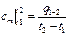Газдар үшін жылыту және суыту кезіндегі тұрақты көлемдегі және тұрақты қысымдағы газ күйінің өзгерістері ерекше ескеріледі: Жылусыйымдылық жылудың берілу және әкетілу түрінен тәуелді. Тұрақты қысымдағы жылусыйымдылық- изобаралық с_р-деп аталады. 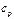, Дж/(кг×К); 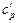, Дж/(м³×К); 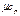, Дж/(кмоль×К). Тұрақты көлемдегі жылусыйымдылық- изохоралық с_v деп ажыратылады. 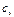, Дж/(кг×К); 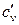, Дж/(м³×К); 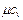, Дж/(кмоль×К). Бұл жылусыйымдылықтардың өзара байланысын Майер теңдеуі көрсетеді: 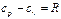мұндағы-R –газ тұрақтысы, Дж/(кг×К) немесе

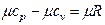
мұндағы 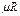- универсалды газ тұрақтысы, 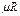= 8314 Дж/(кмоль×К). Изохоралық процесте берілетін жылу тек газды ішкі энергиясын өзгертуге жұмсалады, ал изобаралық процесте ол жылу жұмыс жасау үшін де жұмсалады. Сондықтан с_р>с_v.

Билет

1.Конденсаторлар және оның сиымдылықтары.

Конденсатор деп жұқа диэлектрик қабатымен бөлінген екі өткізгіштен тұратын жүйені айтамыз. Ол латынның “condenso”- қоюлату, жинақтау деген сөзінен шыққан. Конденсатор электр энергиясын және электр зарядтарын жинақтау үшін қолданылады. Конденсатордың екі өткізгішін оның жапсарлары деп атайдың Ол жапсарларды шамасы жағынан тең, таңбалары жағынан қарама –қарсы зарядтпен зарядтайды.Бұл құрал өзіміз көріп жүрген телевизорларда, радиоқабылдағыштарда, магнитофонда және т.б электр
құралдарында қолданылады. Конденсатордың негізгі сипаттамасы оның электрсыйымдылығы болып табылады. Ол конденсатордың электрзарядын жинақтау қабілетін көрсетеді. Сыйымдылықтың анықтамасы бойынша конденсатордың жапсарларындағы заряд оның жапсарларының арасындағы кернеуге тура пропорционал. Конденсатордың сыйымдылығы әдетте 1 пФ –тан жүздеген мкФ –қа дейін, сонымен бірге сыйымдылығы ондаған Ф –қа дейінгі конденсаторлар да кездеседі.
Сонымен қатар конденсаторларды жапсарларының пішініне қарай жазық, цилиндр тәріздес, шар тәріздес және т.б деп бөледі.
Егер өткізгіштер жазық болса және параллель орналасса, онда конденсатор жазық деп аталады.
Жазық конденсатор: С 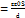Цилиндр тәріздес конденсатор: С= 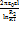Шар тәріздес конденсатор: С = 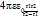1. Сыйымдылықты арттыру үшін конденсаторларды параллель қосады. Бұл кезде конденсаторлардың аттас зарядталған жапсарлары бірге қосылады.
Параллель жалғағанда кернеу бірдей және тізбектің кернеуіне тең, яғни
U=U1=U2=…=Un
С=С1+С2 немесе С=C1+C2+…+Cn 2. Конденсаторларды тізбектей жалғаған кезде барлық конденсаторлардағы заряд бірдей болады және олардың әр аттас зарядталған жапсарлары қосылады.

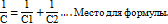
2.Ядролық күштер және оның ерекшеліктері.

Ядролық күштер, атом ядросын құрайтын нуклондардың арасына әсер ететін және ядроның құрылысы мен қасиеттерін (электрмагниттік күштермен бірге) анықтайды. Ядролық күштердің басқа күштерден (мысалы, гравитациялық және электр-магниттік күштер) өзгеше қасиеттері бар. Оларды қысқаша айтсақ төмендегідей: 1) ядродағы нуклондар арасында әсер ететін күштің шамасы атомның электрондық қабықтарында әсер ететін күштің шамасынан әлдеқайда артық. Сондықтан да нуклонды атом ядросынан сыртқа қарай бөлініп шығару үшін млн-даған эВ-қа тең энергия жұмсалуы керек. 2) Ядролық күштер электр-магниттік және гравитациялық күштерге қарағанда өте қысқа қашықтыққа әсер ететін күш болып есептеледі. Егер екі нуклонның арасындағы қашықтық 10–13 см-ден асса, онда ядролық күштердің шамасы нөлге дейін кемиді. Нуклондар арасындағы қашықтық артқан жағдайда, Ядролық күштердің шамасы кеми бастайды. Ядролық күштердің кенет кеми бастайтын қашықтығын ядролық күштердің әсер ету радиусы (r0~2–3× ×10–13 см) деп атайды. 3) Ядродағынуклондар өзіне жақын орналасқан нуклондармен ғана әсерлеседі. Ядролық заттың тығыздығы әр түрлі ядрода да шамамен бірдей. 4) Нуклондар арасындағы өзара әсер күші қашықтыққа ғана байланысты емес, сонымен бірге нуклондар спиндерінің бағдарлануына да байланысты. 5) Ядролық күштердің шамасы өзара әсерлесетін нуклондардың электрзарядына тәуелді емес. Ядролық күштердің дәйекті теориясы әзірше жасалып біткен жоқ. Алайда тәжірибелер ядродағы нуклондардың өзара әсерлері пиондар алмасу арқылы жүзеге асатынын дәлелдейді.

Билет

1.Электромагниттік тербелістер,тербелмелі контур және оның периоды.

Электромагниттік тербелістер - Зарядтың, ток күшінің және кернеудің периодты өзгерісін атайды. Электромагниттік тербеліс кезінде электр және магнит өрістері энергиясының бір-біріне периодты айналу процесі жүреді. Электромагниттік тербелістерді бақылау үшін электрондық осциллограф қолданылады Тербелмелі контур деп бір-біріне тізбектей жалғанған конденсатор мен индуктивті катушкадан тұратын тізбекті атайды. Егер тебелмелі контурдың R кедергісі ескерілмесе, онда ол идеал деп аталады. L индуктивтілік пен С сыйымдылықтан тұратын идеал контурда периоды 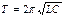Томсон формуласымен, ал меншікті циклдік жиілігі мен жиілігі сәйкесінше 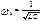, формулаларымен анықталатын меншікті электромагниттік тербелістер пайда бола алады. Конденсаторлардың астарларындағы заряд тербелістерінің теңдеуі былай анықталынады: 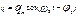Конденсатордағы кернеу тербелістерінің теңдеуі: 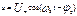Катушкадағы ток тербелістерінің теңдеуі: Конденсатордағы электр өрісі энергиясының ең үлкен мәні: Бұл энергия толығымен катушкадағы магнит өрісінің максимал энергиясына айналады: .

2.Радиоактивтілік.Радиоактивтіліктің ыдырау заңы.Жартылай ыдырау периоды.

Радиоактивтілік (лат. radіo – сәуле шығару, actіvus – әсерлік) – орнықсыз атом ядроларының басқа элементтер ядросына бөлшектер немесе гамма-кванттар шығару арқылы өздігінен түрлену құбылысы. Радиоактивті ыдырау заңы — атом ядроларының әр түрлі бөлшектер мен сәулелер шығара отырып, өздігінен түрлену заңы.^[1][2] Радиоактивті ыдырау заңын Резерфорд ашқан:

немесе Эксперименттік зерттеулер радиоактивті ыдырау толығымен статистикалық заңдылыққа бағынатынын дәлелдеді. Белгілі бір радиоактивті изотоптың ядролары бірдей болады. Атом ядросының және ядролардың қайсысының ыдырайтыны - кездейсоқ оқиға. Мысал үшін, бір нуклидтің бірдей екі ядросын алайық. Ядроның біреуі 3 млрд жыл бұрын жұлдыздың қопарылысы кезінде, ал екінші ядро ядролық реакторда 3 мин бұрын пайда болсын. Ядролардың пайда болу уақытына қарамастан, келесі бір уақыт мезетінде екеуінің де ыдырауының ықтималдығы бірдей. Статистикалық құбылыстарды сипаттау үшін оқиғаның ықтималдығы ұғымын қолданады. Радиоактивті ядролар санының жартысы ыдырайтын уақыт аралығын жартылай ыдырау периоды 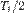деп атайды. Демек, радиоактивті ядролардық алғашкы саны болса, уақыт өткеннен кейін олардың саны 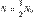болады. (8.11) өрнектен 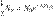аламыз.Осы тендеуді логарифмдесек, , бұдан шығатыны . 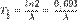Ал 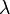тұрақты шама болғандықтан, жартылай ыдырау периоды тұрақты. Радиоактивті ыдырау заңын 1902 жылы Э. Резерфорд пен Ф.Содди ашқан. Есептеулер радиоактивті ядроның орташа өмір сүру уақытын 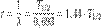өрнегі арқылы анықтауға болатынын көрсетті. Ядроның орташа өмір сүру уақыты жартылай ыдырау периодына пропорционал. Радиоактивті ядроның ыдырау қасиетін сипаттайтын тағы бір шаманы айтуға болады. Уақыт бірлігі ішінде ыдырайтын ядролар санымен анықталатын шаманы радиоактивті заттың активтілігі () деп атайды: 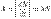Активтіліктің Халықаралық жүйедегі () өлшем бірлігі — беккерель. 1 беккерель (Бк) — уақыт бірлігі 1 с ішінде бір ыдырау болатын радиоактивті препараттың активтілігі: 1 Бк = 1 ыдырау / 1 c. Іс жүзінде қолданылатын активтіліктің басқа да өлшем бірлігі бар, ол — кюри (Ки):1 Ки = 3,7 · 1010Бк; 1 мКи = 3,7 · 10⁷Бк.

Билет

1.Интерференция құбылысы.Когеренттік толқындар және оны алу әдісі.

Фазалар ығысуы тұрақты және жиіліктері бірдей толкындардың қосылуы жарық толқындарының өзара әрекеттесуіндегі көңіл аударатын жағдай. Мұнда кеңістіктің кейбір нүктелерінде толқындардың қабаттасуынан бір-бірін күшейтетін, ал басқа бір нүктелерінде керісінше бір-бірін әлсірететін интерференция құбылысы байқалады. Экранда күңгірт және ашық жолақтар кезектесіп орналасады. Бұл интерференция құбылысы. Жарықтың интерференциясы механикалық толқындардың интерференциясы сияқты өтеді. Жарықтың минимум (әлсіреу) және максимум (күшею) шарттары (4.10) және (4.11) формулаларымен анықталады. Сонымен қатар жарық толқындары интерференциясының кейбір ерекшеліктері бар. Егер екі жарық көзінен бірдей жиілікті синусоидалық жарық толқындары шығарылса, онда олар кездескен жерде интерференция көрінісі пайда болады. Бірақ осы көріністі бір-біріне қатысы жоқ бірдей жарық шығаратын екі жарық көзінен шық қан толқындар арқылы алу мүмкін емес. Жарық толқындарының интерференция құбылысы жоқ деген қорытындыға келгендей боламыз.Интерференция құбылысын 1675 жылы Томас Юнг Ньютон, одан кейін Юнг және Френель байқаған. Мұны қалай түсіндіруге болады? Шын мәнінде, мәселе толқынның цугінде екен. Дененің әр түрлі атомдары бір-біріне байланыссыз жарық шығарады. Сондықтан олардың жиіліктерінің бірдей болуына қарамастан, әр цугтің фазасы әр түрлі. Ал бұл жарықтың фазасы ретсіз өзгеретін электромагниттік толқын екенін көрсетеді. Сонда екі толқынды бір-біріне қосқанда пайда болған қорытқы толқынның берілген нүктедегі амплитудасы да кездейсоқ түрде бір секундта миллион есе (максимум немесе минимум болып) өзгеріп отырады. Жарық түскен бет біздің көзімізге біркелкі жарық түскен беттей болып көрінеді. Сондықтан жарық толқынының интерференциясы тек когерентті толқындар қабаттасқанда ғана пайда болады. Когеренттік (лат. сohaerens – байланыста тұрған) – бір-бірімен қосылған бірнеше тербелмелі не толқынды процестердің уақыт пен кеңістікте үйлесімді өтуі.Егер тербеліс фазаларының айырмасы уақыт бойынша тұрақты әрі ол қосынды тербелістің амплитудасын анықтайтын болса, онда мұндай тербелістер когерентті тербелістер деп аталады (мысалы, жарық толқындарының Когеренттігі). Бірдей жиіліктегі екі гармониялық (синусоидалық) тербеліс әрқашан когерентті болады. Когеренттік электрмагниттік толқындарда да байқалады. Когерентті толқындар қосылған кезде бір-бірін күшейтеді не әлсіретеді (толқын интерференциясы байқалады). Когерентті толқын — егер екі толқынның тербеліс жиілігі мен тұрақты фаза ығысуы бірдей болса, олар когерентті толқындар деп аталады. 2.Электр тогы.Ток күші.Ток тығыздығы.

Электр тогы (Э.т) – электр қозғаушы күштің әсерінен зарядтардың (зарядталған бөлшектер немесе дене) бағытталған қозғалысы. Бұл зарядталған бөлшектер: өткізгіштерде —электрондар, электролиттерде —иондар (катиондар мен аниондар), газда —иондар мен электрондар, арнайы жағдайдағы вакуумда — электрондар, жартылай өткізгіштерде —электрондар мен кемтіктер (электронды-кемтіктік өтімділік) болып табылады.Электр тогы энергетика саласында — энергияны алыс қашықтыққа жеткізу үшін, ал телекоммуникация саласында — ақпаратты шалғайға тасымалдау үшін қолданылады. Электр тогының бағыты шартты түрде өткізгіштердегі оң заряд тасушылардың орын ауыстыру бағыты алынады, бірақ өткізгіштердегі заряд тасушылардың заряды теріс (мысалы, металда электрон) болғандықтан ток бағыты электрондардың бағытына қарсы келеді. Токтың тұрақты ток және айнымалы ток деп аталатын екі түрі бар. Ток күші. Амперметр - Электр тогын өлшеу және салыстыру үшін ток күші деген арнайы шама енгізіледі. Көлденең қимасының ауданы S өткізгіште электр өрісінің әсерінен кейін заряд тасымалдаушылар қандай да бір жылдамдықпен қозғалады деп алайық. Барлық заряд тасымалдаушылардың қозғалысы реттелген болғандықтан, өткізгіш бойымен электр тогы жүреді. Бұл кезде әр секунд сайын өткізгіштің кез келген қимасы арқылы электр мөлшері деп аталатын қандай да бір заряд өтеді. Өткізгіштің көлденең қимасы арқылы қандай да бір уақыт аралығында тасымалданатын электр мөлшерінің сол уақыт аралығына қатынасын ток күші деп атайды: I=q/t. Халықаралық бірліктер жүйесінде (SI) ток күші ампермен (А) өрнектеледі: 1А=1КЛ/1с 1ампер = (1Кулон/(1 секунд)). Ампер - негізгі бірліктердің бірі Электр тоғының тығыздығы – электр тогының векторлық сипаттамасы. Э. т. т. векторының модулі – зарядтың қозғалу бағытына перпендикуляр бірлік аудан арқылы бірлік уақыттың ішінде өтетін электр зарядына тең. Егер зарядтың тығыздығы (бірлік көлеміндегі заряд) r-ға тең болса, онда Э. т. т.: j= ru, мұндағы u – зарядтардың реттелген орын ауыстыруының орташа жылдамдығы. Егер Э. т. т. өткізгіш қимасы бойынша бір қалыпты таралса, онда ток күші (І) мынаған тең: І=jS, мұндағы S – өткізгіштің қимасының ауданы.

Билет

1.Атом құрылысы.Резерфорд тәжірибесі.

Атом бүтіндей алғанда зарядсыз, бейтарап бөлшек. Ол ортасында өзінен радиусы 10⁴ -10⁵ есе кіші көлемді алып жатқан оң зарядты ядродан және оны айнала қозғалып жүрген теріс зарядты электрондардан тұрады. Атом өзінің сыртқы бір немесе бірнеше электрондарын жоғалтқанда оң, ал сырттан электрон қосып алғанда теріс ионға айналады. Атомның сызықтық өлшемдері ~ 10^-8см, көлденең қимасының ауданы ~10^-16 см², көлемі ~10^-24 см³ Атомның массасы, негізінен оның ядросының массасына тең және ол массалық санға (А), яғнипротондар мен нейтрондардың жалпы санына (нуклондардың жалпы санына) пропорционал болып ұлғаяды. Өйткені атомдағы электронның массасы (0.91*10^-20 г) бір протонның немесе нейтронның массасынан (1.67*10^-24 г) 1.840 есе аз. Атомның алғашқы үлгілерінің бірін Дж. Томсон ұсынды. Бұл үлгіде атом радиусы ~10^-10К)м оң зарядталған шар ретінде қарастырылады. Шардың ішінде тепе-теңдік жағдайыныңмаңында электрондар тербеліп тұрады. Электрондардың теріс зарядтарының қосындысы шарға біркелкі таралған оң зарядты теңестіреді, сондықтан тұтас алғанда атом электрлік бейтарап бөлшек болады. Кейінгі зерттеулер бұл модельдің дұрыс емес екенін көрсетті, сондықтан Томсон моделі қазір тек тарихи тұрғыдан қарастырылады. Тәжірибеде алынған нәтижелерді зерделей отырып Резерфорд өз моделін ұсынды. Ол атомның оң заряды оның ортасында орналасқан радиусы шамамен 10^-15 м өте аз көлемгежинақталған деген қорытындыға келді. Бұл орталық бөлшекті Резерфорд ядро деп атады. Атомның массасы түгел дерлік ядрода шоғырланған. Ядроны айнала әр түрлі орбиталарменэлектрондар қозғалып жүреді. Ең шеткі электрон орбитасының радиусы атомның радиусына тең, R_a≈10^-10 м. Бұл үлгі Күн жүйесінің құрылымына ұқсайтын болғандықтан, оны атомныңпланетарлық моделі деп те атайды. Модель бойынша атом көлемінің басым көпшілік бөлігі "бос" болып шығады, ядроның радиусы атомның радиусынан 100 000 есе кіші. Орбиталардағы электрондардың теріс зарядтарының қосындысы ядроның оң зарядына тең, атом электрлік бейтарап. Атомның ішіндегі бос кеңістік "өте үлкен". Сондықтан, фольга арқылы өткенде альфа-бөлшектерінің көбі ядродан алыс өтеді де, шашырамайды. Электрондар альфа-бөлшектен 8 мың еседей жеңіл болғандықтан, оның қозғалыс траекториясын өзгерте алмайды. Тек ядроға тікелей қарсы келіп қалған альфа-бөлшектер ғана онымен әсерлесіп, кері ұшады. Мұндай бөлшектер саны ядро радиусының атом радиусына қатынасымен анықталады.

2.Магнит өрісінің қозғалыстағы заядқа әсері.Лоренц күші және оның бағытын анықтау.

Магнит өрісі тек тоғы бар өткізгішке ғана емес, сол сияқты кез келген қозғалыстағы зарыдтарға да әсер ететіндігін көптеген эксперименттердің нәтижелері дәлелдеді. Ал магнит өрісіндегі әр зарядқа әсер ететін күшті Лоренц күші деп атайды. Енді осы Лоренц күшін табайық. Ол үшін біртекті магнит өрімінде ұзындығы l тоғы бар өткізгіш алайық. Өткізгіш магниит өрісінің бағытына бұрышпен орналасқан. Өткізгішке ток теріс зарядты электрондардың бағытталған қозғалысы болғандықтан, осы зарядқа әсер етуші күштерді анықтайық. Тоқтың бір элементін бөліп алып оған әсер етуші күшті Ампер заңына сәйкес жазайық:
F = IB ∆ l sin
мұндағы I - өткізгіштегі ток күші. Электрондық теорияға сәйкес ток шамасы мынаған тең:
I = eno S,
Мұндағы е – электрон заряды, no - өткізгіштің бірлік көлеміндегі еркін электрондардың саны, - электрондардың бағытталған жылдамдығы, S - өткізгіштің көлденең қимасының ауданы.
Енді осы тоқтың мәнін жоғарғы формулаға қойсақ, онда ол мынандай түрге келеді:
F = В eno S ∆ l sin
Әрбір жеке зарядқа әсер ететін Лоренц күшін табу үшін ∆ l элементтегі еркін электрондардың санын есептеу керек. Оны анықтау үшін көлденең қимасы S, ∆ l элементтегі барлық электрондар санын анықтаймыз n = no∆ lS
Сонда Лоренц күші мына қатыс арқылы есептелінеді:

Осы өрнекті бірінші рет голланд физигі Лоренц (1853-1928) шығарған болатын, сондықтан оны Лоренц күші (Fл) деп атайды. Мұндағы - магнит өрісінң күш сызықтары мен электрондардардың бағытталған жылдамдығының арасындағы бұрыш. Лоренц күшінің бағытын сол қол ережесі бойынша анықтайды, яғни магниит индукциясы алақанды тесіп өтсе, саусақтар электрондар жылдамдығының бағытын көрсетсе, онда бас бармақ Лоренц күшінің бағытын анықтайды. Сонымен, Лоренц күші электрондардың жылдамдығына перпендикуляр болып, оларға нормаль үдеу беріп отырды. Лоренц күші магнит өрісінде ешқандай жұмыс істемейді. Күш тек электрондардың жылдамдығының бағытын ғана өзгертеді. Олай болса жылдамдықтың шамасы мен кинетикалық энергиясы магнит өрісінде өзгермейді. Жалпы магниит өрісіндегі қозғалыстағы зарядқа магнит идукциясынан басқа, кернеулігі электр өрісі де әсер етеді. Олай болса, зарядқа әсер етуші қорытқы күш электрлік күш пен Лоренц күшінің қосындысына тең болады. Тағы да бір ескертетін жағдай, магнит өрісі еш уақытта тыныштықта тұрған электр зарядына әсер етпей, тек қана қозғалыстағы зарядтарға ғана әсер етеді. Бұл тұрғыда магнит өрісінің электр өрісінен ерекшелігінің бар екенідігін байқауға болады.

Не нашли, что искали? Воспользуйтесь поиском: