
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Квадратные уравнения. Теорема Виета
Уравнение вида  , где x – переменная, a, b, c – некоторые числа, причем, а ≠ 0, называется квадратным.
, где x – переменная, a, b, c – некоторые числа, причем, а ≠ 0, называется квадратным.
а – первый коэффициент;
b – второй коэффициент;
с – свободный член.
Квадратные уравнения, в которых хотя бы один из коэффициентов b или с равен нулю, называются неполными.

| 
| 
|
 1) Если ас > 0 – корней нет
2) Если ac < 0
1) Если ас > 0 – корней нет
2) Если ac < 0  
| 
| x=0 |
Выведем формулу корней квадратного уравнения. Для этого решим уравнение  , где а ≠ 0. Разделим все его члены на а. Получим равносильное уравнение:
, где а ≠ 0. Разделим все его члены на а. Получим равносильное уравнение:  (2).
(2).
Выделим полный квадрат:  .
.
Тогда уравнение (2) примет вид 
или  (3).
(3).
Число корней зависит от знака дроби  , т.к. а ≠ 0, то
, т.к. а ≠ 0, то 
 знак определяется выражением
знак определяется выражением  . Обозначим его D =
. Обозначим его D =  и назовем дискриминантом. Тогда уравнение (3) перепишется в виде:
и назовем дискриминантом. Тогда уравнение (3) перепишется в виде:  (4). Рассмотрим случаи:
(4). Рассмотрим случаи:
| D < 0 | D = 0 | D > 0 |
 , но , но
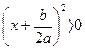 для любого действительного x.
Значит, корней нет. для любого действительного x.
Значит, корней нет.
| 
 Значит, два равных корня
Значит, два равных корня  . .
|  то то 


 или или   или или  Значит, два различных корня
Значит, два различных корня 
 , где
D = , где
D = 
|
При решении квадратного уравнения, в котором второй коэффициент
b – четное число, используют следующую формулу:
 , где
, где  .
.
Квадратное уравнение, первый коэффициент которого равен 1, называется приведенным:  . Корни приведенного квадратного уравнения можно найти по формулам:
. Корни приведенного квадратного уравнения можно найти по формулам:  ;
;
 .
.
Теорема Виета: Сумма корней квадратного уравнения  равна
равна  , произведение корней равно
, произведение корней равно  .
.
Доказательство:

Теорема доказана.
Следствие: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену: 
Обратная теорема: Если числа x1 и x2 такие, что  , то они являются корнями квадратного уравнения
, то они являются корнями квадратного уравнения  .
.
Определение знаков корней квадратного уравнения.
| Оба положительны | Оба отрицательны | Одного знака | Разных знаков |

| 
| 
| 
|
Уравнение 4-ой степени вида 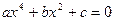 , где а ≠ 0, называется биквадратным.
, где а ≠ 0, называется биквадратным.
Не нашли, что искали? Воспользуйтесь поиском: