Уравнения с несколькими неизвестными. Системы уравнений

Уравнение вида f(x; y)=0 называется уравнением с двумя переменными.

Решением уравнения с двумя переменными называется пара значений переменных, обращающих уравнение в верное равенство. Обычно решение записывают в виде пары чисел (x₀; y₀).

Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное числовое равенство.

Уравнение вида , где x, y – переменные, a, b, c – действительные числа, называется линейным.

Если ставится задача найти все общие решения двух уравнений с двумя переменными, то говорят, что надо решить систему уравнений.

Решением системы уравнений с двумя переменными называется пара значений переменных, удовлетворяющих каждому из уравнений.

Решить систему уравнений – значит найти все ее решения или установить, что их нет.

Две системы уравнений называют равносильными, если они имеют одни и те же решения.

Система линейных уравнений с двумя переменными имеет вид .

Не решая систему линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

1. Если 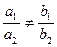, т.е. коэффициенты при x и y не пропорциональны, то система имеет одно решение. Графически – прямые пересекаются.

2. Если , т.е. коэффициенты при x и y пропорциональны, а свободные члены нет, то система не имеет решений. Графически – прямые параллельны.

3. Если , т.е. все коэффициенты пропорциональны, то система имеет множество решений. Графически – прямые совпадают.

Методы решения систем уравнений:

1. Метод подстановки.

2. Метод алгебраического сложения.

3. Графический метод.

4. Метод введения новых переменных.

Не нашли, что искали? Воспользуйтесь поиском: