Свойства бесконечно малых последовательностей

1. Бесконечно малая последовательность ограничена.
2. Сумма бесконечно малых последовательностей есть бесконечно малая последовательность.
3. Произведение бесконечно малой последовательности на ограниченную есть бесконечно малая последовательность.
4. Если элементы бесконечно малой последовательности 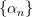равны одному и тому же числу , то .

14) Понятие предела числовой последовтельности

Число a называется пределом последовательности x = { x_n }, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство |x_n - a| < ε.

15) Единственность предела

Теорема: (о единственности предела последовательности)

Числовая последовательность может иметь только один предел.

Предположим, что последовательность 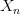имеет два различных предела b и a, причем b < a. Выберем 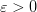таким, чтобы -oкрестности точек b и a не пересекались (не имели общих точек). Возьмем, например, . Так как число b — предел последовательности 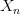, то по заданному 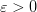можно найти номер N такой, что для всех 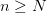. Поэтому вне интервала 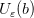может оказаться лишь конечное число членов последовательности. В частности, интервал 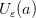может cодержать лишь конечное число членов последовательности. Это противоречит тому, что a – предел последовательности (любая окрестность точки a должна содержать бесконечное число членов последовательности). Полученное противоречие показывает, что последовательность не может иметь два различных предела. Итак, сходящаяся последовательность имеет только один предел.

16) Ограниченность сходящейся последовательности

Последовательность 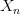называется ограниченной снизу, если существует такое число , что все члены последовательности удовлетворяют условию 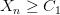, т. е.:

Последовательность 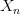называется ограниченной сверху, если:

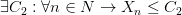
Последовательность, ограниченную как снизу, так и сверху, называют ограниченной, т. е. последовательность 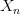называется ограниченной, если:

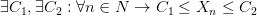
это можно записать и так:

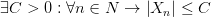
Таким образом, последовательность называют ограниченной, если множество ее значений ограничено.

Примеры.

Теорема: (об ограниченности сходящейся последовательности)

Если последовательность имеет предел, то она ограничена.

Доказтельство:

Пусть последовательность 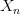имеет предел, равный а. По определению предела для найдем номер N такой, что при всех 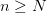имеет место неравенство . Так как модуль суммы не превосходит суммы модулей, то:

.

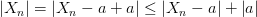Поэтому при всех 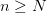выполняется неравенство:

.

Положим 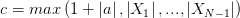, тогда 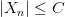при всех , т. е. последовательность 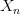ограничена.

Замечание: В силу предыдущей теоремы всякая сходящаяся последовательность является ограниченной. Обратное неверно: не всякая ограниченная последовательность является сходящейся! Например, последовательность ограничена, но не является сходящейся.

Замечание: Если условие 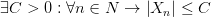не выполняется, т. е.

,

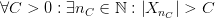то говорят, что последовательность 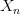не ограничена.

17) Предел суммы, разности, произведения и частного последовательностей

Если две последовательности { x_n } и { y_n } имеют пределы, равные соответственно a и b, то:

а) Последовательность { x_n 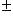y_n } имеет предел равный a 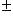b, т. е.

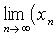
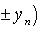
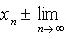
Это свойство распространяется на случай любого фиксированнго числа слагаемых.

б) Последовательность { x_n y_n } имеет предел равный ab, т. е.

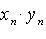
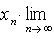
Это свойство распространяется также на случай любого фиксированного числа сомножителей.

Постоянный множитель можно выносить за знак предела при любом постоянном k.

с) Последовательность 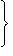имеет предел равный 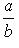, т. е.

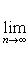
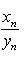
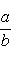
при условии, что все y_n не равны нулю и .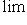

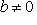18) Предельный переход в неравенстве

Теорема. Если элементы сходящейся последовательности { x_n }, начиная с некоторого номера, удовлетворяют неравенству x_n ≥ b (x_n ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).

Доказательство. Пусть все элементы x_n, по крайней мере начиная с некоторого номера, удовлетворяют неравенству x_n ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности { x_n }, то для положительного ε = b - a можно указать номер N такой, что при n ≥ N выполняется неравенство | x_n - a | < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < x_n - a < b - a. Используя правое из этих неравенств, получим x_n < b, а это противоречит условию теоремы. Случай x_n ≤ b рассматривается аналогично. Теорема доказана.

Замечание. Элементы сходящейся последовательности { x_n } могут удовлетворять строгому неравенству x_n > b, однако при этом предел a может оказаться равным b. Например, если 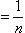, то x_n > 0, однако .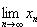

Следствие 1. Если элементы x_n и y_n сходящихся последовательностей { x_n } и { y_n }, начиная с некоторого номера, удовлетворяют неравенству x_n ≤ y_n, то их пределы удовлетворяют такому же неравенству:

В самом деле, элементы последовательности { y_n - x_n } неотрицательны, а поэтому неотрицателен и ее предел 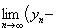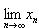. Отсюда следует, что

19) Теорема о двух милиционерах

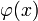Если функция такая, что для всех в некоторой окрестности точки , причем функции и 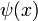имеют одинаковый предел при , то существует предел функции при , равный этому же значению, то есть

20) Теорема Вейерштрасса для последовательности

Не нашли, что искали? Воспользуйтесь поиском: