
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Эквивалентность определений
Пусть число  является пределом функции
является пределом функции 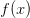 в точке
в точке  по Коши. Выберем произвольную подходящую последовательность
по Коши. Выберем произвольную подходящую последовательность  ,
,  , то есть такую, для которой
, то есть такую, для которой 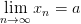 . Покажем, что
. Покажем, что  является пределом по Гейне.
является пределом по Гейне.
Зададим произвольное 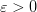 и укажем для него такое
и укажем для него такое  , что для всех
, что для всех  из условия
из условия  следует неравенство
следует неравенство  . В силу того, что
. В силу того, что 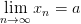 , для
, для  найдётся такой номер
найдётся такой номер  , что
, что  будет выполняться неравенство
будет выполняться неравенство  , то есть
, то есть 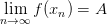 .
.
Докажем теперь обратное утверждение: предположим, что  по Гейне, и покажем, что число
по Гейне, и покажем, что число  является пределом функции
является пределом функции 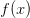 в точке
в точке  по Коши. Предположим, что это неверно, то есть:. В качестве
по Коши. Предположим, что это неверно, то есть:. В качестве 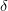 рассмотрим
рассмотрим  , а соответствующие значения
, а соответствующие значения  будем обозначать
будем обозначать  . Тогда при любом
. Тогда при любом  выполняются условия
выполняются условия  и
и 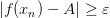 . Отсюда следует, что последовательность
. Отсюда следует, что последовательность  является подходящей, но число
является подходящей, но число  не является пределом функции
не является пределом функции 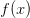 в точке
в точке  . Получили противоречие.
. Получили противоречие.
Примеры
Пример 3.1.
а) 

 , например
, например 
б) 

Пример 3.2.
Доказать, что  не имеет предела в точке 0.
не имеет предела в точке 0.





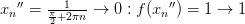
Вывод: последовательность по Гейне не имеет предела.
27) Критерий Коши существования предела функции в точке.
Теорема 5 (критерий Коши). Для того чтобы функция f, x  X, имела в (конечной или бесконечно удаленной) точке x 0 конечный предел, необходимо и достаточно, чтобы для любого
X, имела в (конечной или бесконечно удаленной) точке x 0 конечный предел, необходимо и достаточно, чтобы для любого  > 0 существовала такая окрестность U (x 0) точки x 0, что для любых x'
> 0 существовала такая окрестность U (x 0) точки x 0, что для любых x'  X
X  U (x 0) и x"
U (x 0) и x"  X
X  U (x 0) выполнялось бы неравенство
U (x 0) выполнялось бы неравенство
| f (x") - f (x')| <  . .
| (6.39) |
 Докажем необходимость условия (6.39). Пусть
Докажем необходимость условия (6.39). Пусть  f (x) = a
f (x) = a  R, тогда для любого
R, тогда для любого  > 0 существует такая окрестность U (x 0) точки x 0, что для каждого x
> 0 существует такая окрестность U (x 0) точки x 0, что для каждого x  X
X  U (x 0) справедливо неравенство
U (x 0) справедливо неравенство
| f (x) - a | <  /2.
/2.
Поэтому если x'  X
X  U (x 0)и x"
U (x 0)и x"  X
X  U (x 0), то
U (x 0), то
| f (x") - f (x')| = |[ f (x") - a ] + [ a - f (x')]| <
< | f (x") - a | + | a - f (x')| <  /2 +
/2 +  /2 =
/2 =  .
.
Докажем достаточность условий (6.39) для существования конечного предела  f (x). Пусть произвольно фиксировано
f (x). Пусть произвольно фиксировано  > 0; тогда существует такая окрестность U (x 0), что для всех x'
> 0; тогда существует такая окрестность U (x 0), что для всех x'  X
X  U (x 0) и всех
U (x 0) и всех
x"  X
X  U (x 0) выполняется неравенство | f (x") - f (x')| <
U (x 0) выполняется неравенство | f (x") - f (x')| <  . Возьмем какую-либо последовательность xn
. Возьмем какую-либо последовательность xn  x 0, xn
x 0, xn  X, n = 1, 2,... В силу определения предела последовательности существует такой номер n 0, что для всех
X, n = 1, 2,... В силу определения предела последовательности существует такой номер n 0, что для всех
n > n 0 имеет место включение xn  U (x 0), а поскольку xn
U (x 0), а поскольку xn  X, то и включение xn
X, то и включение xn  X
X  U (x 0). Тогда для всех номеров n > n 0 и m > n 0 будем иметь xn
U (x 0). Тогда для всех номеров n > n 0 и m > n 0 будем иметь xn  X
X  U (x 0), xm
U (x 0), xm  X
X  U (x 0), и, следовательно, будет выполняться неравенство | f (xn) - f (xm)| <
U (x 0), и, следовательно, будет выполняться неравенство | f (xn) - f (xm)| <  . Это означает, что последовательность { f (xn)} удовлетворяет критерию сходимости Коши для последовательностей и, следовательно, имеет конечный предел.
. Это означает, что последовательность { f (xn)} удовлетворяет критерию сходимости Коши для последовательностей и, следовательно, имеет конечный предел.
Таким образом, для любой последовательности xn  x 0, xn
x 0, xn  X, n = 1, 2,..., последовательность { f (xn)} имеет конечный предел. Отсюда в силу леммы 2 п. 6.4 сразу следует, что функция f имеет в точке x 0 конечный предел.
X, n = 1, 2,..., последовательность { f (xn)} имеет конечный предел. Отсюда в силу леммы 2 п. 6.4 сразу следует, что функция f имеет в точке x 0 конечный предел. 
Замечание. Сформулируем критерий Коши существования конечного предела функции в терминах неравенств для случая, когда x 0 - действительное число: функция f, x  X, имеет в точке x 0
X, имеет в точке x 0  R конечный предел тогда и только тогда, когда для любого
R конечный предел тогда и только тогда, когда для любого  > 0 существует такое
> 0 существует такое  > 0, что для всех точек
> 0, что для всех точек
x'  X, x"
X, x"  X, | x' - x 0| <
X, | x' - x 0| <  , | x" - x 0| <
, | x" - x 0| <  , выполняется неравенство | f (x") - f (x')| <
, выполняется неравенство | f (x") - f (x')| <  .
.
28) Предел суммы, разности, произведения и частного функций.
1)Предел суммы двух функций равен сумме их пределов:  .
.
Доказательство:
Пусть  ,
,  . Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать:
. Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать:  и
и  . Следовательно,
. Следовательно,  , где
, где  - бесконечно малая функция (по свойству бесконечно малых функций). Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать
- бесконечно малая функция (по свойству бесконечно малых функций). Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать  , или
, или  .
.
2) Предел произведения двух функций равен произведению их пределов:  .
.
Доказательство:
Пусть  ,
,  . Тогда
. Тогда  и
и  . Следовательно
. Следовательно
 ,
,
 .
.
Выражения в скобках, по свойствам бесконечно малых функций, - бесконечно малая функция. Тогда  , т.е.
, т.е.  .
.
2) Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен:  .
.
Доказательство:
Пусть  ,
,  . Тогда
. Тогда  и
и  . Тогда
. Тогда  . По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция.
. По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция.
Поэтому  , т.е.
, т.е. 
29) Односторонние пределы функции. Непрерывность функции в точке.
Не нашли, что искали? Воспользуйтесь поиском: