Непрерывность функции в точке и на интервале

В той или иной математической задаче речь может идти о непрерывности функции в точке, непрерывности функции на интервале, полуинтервале или непрерывности функции на отрезке. То есть, не существует «просто непрерывности» – функция может быть непрерывной ГДЕ-ТО. И основополагающим «кирпичиком» всего остального является непрерывность функции в точке.

Теория математического анализа даёт определение непрерывности функции в точке с помощью «дельта» и «эпсилон» окрестностей, но на практике в ходу другое определение, которому мы и уделим самое пристальное внимание.

Сначала вспомним односторонние пределы, ворвавшиеся в нашу жизнь на первом уроке о графиках функций. Рассмотрим будничную ситуацию:

Если приближаться по оси 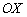к точке 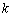слева (красная стрелка), то соответствующие значения «игреков» будут идти по оси 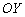к точке 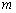(малиновая стрелка). Математически данный факт фиксируется с помощью левостороннего предела:

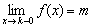
Обратите внимание на запись 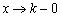(читается «икс стремится к ка слева»). «Добавка» «минус ноль» символизирует бесконечно малое отрицательное число, по сути это и обозначает, что мы подходим к числу 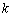с левой стороны.

Аналогично, если приближаться к точке «ка» справа (синяя стрелка), то «игреки» придут к тому же значению 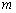, но уже по зелёной стрелке, и правосторонний предел оформится следующим образом:

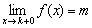
«Добавка» 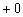символизирует бесконечно малое положительное число, и запись 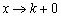читается так: «икс стремится к ка справа».

Если односторонние пределы конечны и равны (как в нашем случае): 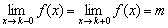, то будем говорить, что существует ОБЩИЙ предел 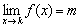. Всё просто, общий предел – это наш «обычный» предел функции, равный конечному числу.

Заметьте, что если функция не определена при (выколите чёрную точку на ветке графика), то перечисленные выкладки остаются справедливыми. Как уже неоднократно отмечалось, в частности, в статье о бесконечно малых функциях, выражения 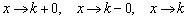означают, что «икс» бесконечно близко приближается к точке 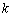, при этом НЕ ИМЕЕТ ЗНАЧЕНИЯ, определена ли сама функция в данной точке или нет. Хороший пример встретится в следующем параграфе, когда анализу подвергнется функция .

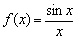Определение: функция непрерывна в точке 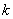, если предел функции в данной точке равен значению функции в этой точке: .

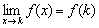Определение детализируется в следующих условиях:

1) Функция должна быть определена в точке 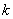, то есть должно существовать значение .

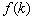2) Должен существовать общий предел функции 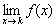. Как отмечалось выше, это подразумевает существование и равенство односторонних пределов: .

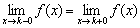3) Предел функции в данной точке должен быть равен значению функции в этой точке: .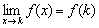

!!! Рекомендую законспектировать пункты, поскольку они потребуются для решения практических задач. Далее по тексту они будут отмечаться как Условие №1, Условие №2 и Условие №3.

Если нарушено хотя бы одно из трёх условий, то функция теряет свойство непрерывности в точке .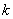

Непрерывность функции на интервале формулируется остроумно и очень просто: функция непрерывна на интервале 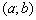, если она непрерывна в каждой точке данного интервала.

В частности, многие функции непрерывны на бесконечном интервале 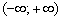, то есть на множестве действительных чисел . Это линейная функция, многочлены, экспонента, синус, косинус и др. И вообще, любая элементарная функция непрерывна на своей области определения, так, например, логарифмическая функция 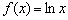непрерывна на интервале 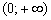. Надеюсь, к данному моменту вы достаточно хорошо представляете, как выглядят графики основных функций. Более подробную информацию об их непрерывности можно почерпнуть у доброго человека по фамилии Фихтенгольц.

С непрерывностью функции на отрезке 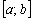и полуинтервалах 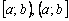тоже всё несложно, но об этом уместнее рассказать на уроке о нахождении минимального и максимального значений функции на отрезке, а пока голову забивать не будем.

30) Классификация точек разрыва функции.

31) Эквивалентность бесконечно малых функций. Первый замечательный предел.

32) Теорема Коши о промежуточных значениях функции, непрерывной на отрезке.

33) Равномерная непрерывность. Теорема Кантора.

34) Свойства функций, непрерывных на отрезке (первая, вторая теорема Вейштрасса)

35) Понятие производной. ЕЕ геометрический и механический смыслы.

36) Непрерывность дифференцируемой функции.

37) Арифметические действия над дифференцируемыми функциями.

38) Таблица производных.

39) Дифференциал, его геометрический смысл. Инвариантность формы первого дифференциала.

40) Основные формулы и правила дифференцирования

41) Производные и дифференциалы высших порядков

42) Теорема Ролля

43) Теорема Коши

44) Теорема Лагранжа

45) Правила Бернулли-Лопиталя

46) Формула Тейлора для многочлена

47) Формула Тейлора для функции

48) Различные представления остаточного члена формулы Тейлора

49) Формула Маклорена. Разложение элементарных функций по формуле Маклорена.

50) Критерий монотонности функции

51) Локальный экстремум. Теорема Ферма.

52) Выпуклые функции. Критерий выпуклости функции.

53) Достаточные условия экстремума функции.

Не нашли, что искали? Воспользуйтесь поиском: