Метод простой итерации

Для решения методом простых итераций каждое уравнение СЛАУ преобразуют таким образом, чтобы в левой части находилась лишь одна из искомых переменных и получают расчетные выражения:

(7)

или в общем виде

. (8)

Задают некоторые значения исходных приближений 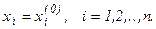Подставляя их в правую часть выражений (5) вычисляют новые приближения 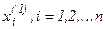, данные приближения используют для получения приближений на второй итерации и т.д.

Очередное k -е приближение считают решением, если исходная система уравнений (1) после подстановки соответствующего набора 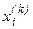“обращается” в тождество с заданной точность e.

Для проверки данного условия необходимо вычислить вектор невязок, элементы которого, очевидно, равны:

(9)

или в матричной форме

r = A×x – b.

Если наибольшая по модулю составляющая вектора невязок удовлетворяет условию max 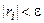, то набор 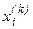считают решением системы.

Если для номера итерации k > 1 максимальная невязка 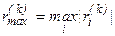больше максимального значения модуля невязки на предыдущей итерации, то расчет “аварийно” завершают. Говорят, что итерационный процесс расходится.

Полезно построить такой алгоритм решения задачи, чтобы определение вектора невязок и вычисление новых приближений требовали минимального числа операций. Добавляя в выражение для каждой из невязок член 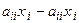, после простейших преобразований получим расчетное выражение, аналогичное (8):

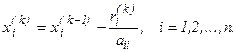, (10)

где невязки определяют по формуле

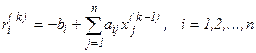. (11)

Алгоритм решения состоит в следующем:

þ 1. Задают начальные значения 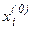, полагают счетчик итераций k=1 . Задают предельное допустимое число итераций k_max по достижению которого расчет должен быть прекращен с целью предотвращения “зацикливания” в случае плохой сходимости итерационного процесса к решению.

þ 2. Полагают начальное значение максимальной невязки на “предыдущей” итерации равным большому числу, предельно допустимому для данной ЭВМ, например .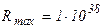

þ 3. Полагают начальное значение максимальной невязки на текущей итерации .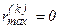

þ 4. Для i=1,2,..n выполняют пункты 5,6,7 данного алгоритма.

þ 5. Вычисляют невязку i -го уравнения по формуле (11).

Если 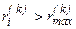, то запоминают .

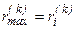þ 6. Вычисляют новое значение i- го неизвестного по формуле (10).

þ 7. Вычислены новые приближения 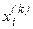для всех n неизвестных. Рассчитывают текущее значение максимальной невязки и определяют условия окончания расчета:

þ 7.1.Если , расчет успешно завершают и переходят к пункту 9 алгоритма, иначе к пункту 7.2.

þ 7.2. Если максимальная невязка увеличилась по сравнению с максимальной невязкой на предыдущей итерации, т.е. 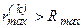, то фиксируют расходящийся процесс, переходят к пункту 8, иначе запоминают 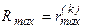и переходят к п 7.3.

þ 7.3. Увеличивают счетчик итераций k=k+1, если k<k_max переходят к пункту 3, иначе к пункту 8 алгоритма.

þ 8. Сообщение об аварийном завершении. Конец расчета.

þ 9. Получены значения 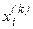. Конец расчета.

Не нашли, что искали? Воспользуйтесь поиском: