
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение дифференциальных уравнений методом Эйлера
Метод численного интегрирования Эйлера предназначен для решения задачи Коши: найти на интервале времени tÎ[T0,T] решение дифференциального уравнения
 (18)
(18)
при заданных начальных условиях:  t(0)=T0 , y(0)=y0.
t(0)=T0 , y(0)=y0.
В результате решения данной задачи получают в форме графика или таблицы значения функции y(t).
Метод Эйлера является дискретным, т.е. таким, посредством которого вычисляется последовательность приближенных значений  на множестве точек tk+1=tk+h, k=0,1,2..., принадлежащих заданному интервалу времени. Здесь h - заданная пользователем величина шага численного интегрирования.
на множестве точек tk+1=tk+h, k=0,1,2..., принадлежащих заданному интервалу времени. Здесь h - заданная пользователем величина шага численного интегрирования.
Геометрическая интерпретация численного интегрирования методом Эйлера приведена на рис. 1.

Рис. 2.
Участок искомой неизвестной функции y(t) “заменяют” касательной к нему прямой (линеаризация функции в окрестности заданной точки). По известным значениям y0, h и вычисленному значению производной, определяющей наклон касательной, можно из треугольника ABC определить значение приращенияфункции D y0 = y1 – y0 =h f(y0,Т0) на отрезке времени длины h.
Тогда значение y1 для момента времени t1 =T0+h можно определить по формуле
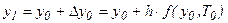 . (19)
. (19)
Полученное значение можно использовать для вычисления по аналогичной формуле значения функции в точке t2=T0+2h=t1+h и т.д. пока не будет достигнут конец заданного интервала интегрирования.
В общем случае расчетная формула метода Эйлера имеет вид
 . (20)
. (20)
Очевидно, что чем меньше величина h, тем ближе полученное значение yk+1 к точному значению неизвестного точного решения y(tk+1). Абсолютная погрешность выполнения шага численного интегрирования не может быть определена, известно лишь что она для данного метода прямо пропорциональна величине h.
В связи с этим разработаны различные процедуры получения оценки локальной погрешности на шаге численного интегрирования, требующие, очевидно, увеличения объема вычислений.
Наиболее простая, достаточно надежная, но не очень эффективная с точки зрения вычислительных затрат процедура оценки точности расчета заключается в следующем:
1.Выполняют один шаг интегрирования величины h, получают значение yk+1 для t=t k+1.
2. Из той же начальной точки выполняют два шага интегрирования и определяют значение  для момента времени t=t k+1.
для момента времени t=t k+1.
3.По разности двух значений, полученных с абсолютной погрешностью, отличающейся вдвое, можно вычислить приближенную оценку D локальной погрешности на k -ом шаге интегрирования:
 (21)
(21)
где p - порядок точности метода численного интегрирования, для метода Эйлера p=1.
4.Если оценка локальной погрешности D больше, чем желаемая пользователем точность расчета e, то величину шага интегрирования необходимо уменьшить и продолжить расчет с новым значением h. Очевидно, что неудачный шаг должен быть повторен из той же исходной точки. Иногда для определения приемлемого значения h необходимо выполнить 2¸3 подобных итерации.
Для выбора величины шага можно использовать формулу
 , (22)
, (22)
где a - коэффициент запаса, значение которого обычно выбирают из диапазона значений 0.5¸ 0..9.
Эту формулу полезно использовать на каждом шаге и в том случае, когда текущая оценка погрешности удовлетворяет заданной точности. При этом возможно будет рекомендовано большее значение h, что позволит сократить общее число необходимых шагов интегрирования.
В случае решения систем дифференциальных уравнений вычисления выполняются по аналогичным формулам. Однако выбор шага осуществляют по наибольшему значению оценки погрешности D.
Задания:
1.Выполнить решение системы дифференциальных уравнений второго порядка методом Эйлера с оценкой погрешности и выбором величины шага интегрирования “вручную” ограничив объем вычислений тремя полными шагами. Построить график изменения функции y(t).
2.Используя программу для расчета на ПЭВМ выполнить трижды численное интегрирование системы дифференциальных уравнений с фиксированным шагом, принимая его значение равным h, 2h, 4h. Построить три расчетных графика изменения функции и сравнить полученные решения.
Варианты исходных данных приведены в табл.1.
Таблица 1
Варианты исходных данных
| № варианта | Система дифференциальных уравнений | Начальные условия |
| 1 | y'= 5x+ 0.2t x'= -y×x - y | t0=0; y0=2; x0=1.5; |
| 2 | y'= x-y x'= (1-y)x+ 0.1t | t0=0; y0=1; x0=1.5; |
| 3 | y'= 2x2- y + 0.5 t x'= -x2- y | t0=0; y0=2; x0=1; |
| 4 | y'= x - 3y x'= -x2+ y×x+ 0.2t | t0=0; y0=1; x0=2; |
| 5 | y'= 5x (1 - y) x'= x -2×y - 0.01t | t0=0; y0=2; x0=3; |
| 6 | y'= -2y - 1/x x'= (3-y)×x2+ 0.3t | t0=0; y0=4; x0=–2; |
| 7 | y'= 5x - y2+ 0.1t x'= (4-y)×x | t0=0; y0=2; x0=5 |
| 8 | y'= 1/x - 3y x'= -5x + 0.2t | t0=0; y0=3; x0=4; |
| 9 | y'= 3x2- y x'= 2(y+1)×x + 0.3t | t0=0; y0=1; x0=3; |
| 10 | y'= x - 5y + 0.01 t x'= (1-y)(3 - x) | t0=0; y0=3 x0=–1 |
| 11 | y'= x×(5 - y)2 x'= (2-x)×y+ 0.4t | t0=0; y0=2.5; x0=2; |
| 12 | y'= x - 4×y2+ 0.1t x'= -y×(2-x) | t0=0; y0=0.5; x0=3 |
| 13 | y'= 4 -y + x+ 0.1t x'= (5-y2)×x | t0=0; y0=3; x0=4; |
| 14 | y'= x2/(5 - y) + t x'= (1-y)(3 - x) | t0=0; y0=0.5; x0=2 |
| 15 | y'= x2- y + 0.2t x'= (1 - y) x2 | t0=0; y0=3; x0=7 |
| 16 | y'= 1/x - y + 0.3t x'= y/(3 - x) | t0=0; y0=2; x0=4 |
| 17 | y'= -x2- y +5 x'= -x + 5y + 0.05t | t0=0; y0= -1; x0=2 |
| 18 | y'= -x (1 + y)2 x'= (2-y)(4 - x) | t0=0; y0=4; x0=1 |
| 19 | y'= 4 - y - 1/x x'= (2 + y2)(3 - x) + 0.05t | t0=0; y0=1; x0=2 |
| 20 | y'= 1 - 2x - yx + 0.13t x'= 2y (1 - x) | t0=0; y0= -3 x0=4 |
| 21 | y'= 3 - y + xy x'= (1 + 2y)(1 - x) + 0.5t | t0=0; y0=2; x0=3 |
| 22 | y'= -y - 5x2– 0.25t x'= y (5 + y - x) | t0=0; y0=2; x0= -1 |
| 23 | y'= (1 - y2)y - x + 0.4t x'= (2 + y) - x | t0=0; y0=–2; x0=2 |
| 24 | y'= -x - 2y + 0.15t x'= (3 + y) x | t0=0; y0= -2; x0= 2 |
| 25 | y'= 1 - y - 5x x'= y - xy + 0.9t | t0=0; y0=3; x0=1 |
Не нашли, что искали? Воспользуйтесь поиском: