
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение систем линейных алгебраических уравнений методом Гаусса
При упоминании метода Гаусса решения СЛАУ часто подразумевают целое семейство алгоритмов, основанных на общей идее упорядоченного исключения неизвестных.
Метод Гаусса является прямым, т.е. требует выполнения заранее известного числа действий, необходимых для того, чтобы получить решение или зафиксировать факт вырожденности (равенства нулю определителя) матрицы коэффициентов при неизвестных. В общем случае для решения системы n уравнений требуется число операций, пропорциональное  .
.
Решение включает в себя два основных этапа. На первом этапе, называемом прямым ходом метода, систему уравнений с матрицей коэффициентов при неизвестных общего вида приводят к специальной форме, например, верхней или нижней треугольной, при этом пересчитывают значения элементов матрицы  и вектора свободных членов
и вектора свободных членов 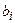 .
.
На втором этапе, называемом обратным ходом, преобразованную к упрощенной форме систему решают каким-либо известным способом, например, методом обратной или прямой подстановки.
Пусть система n линейных алгебраических уравнений с n искомыми неизвестными 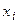 задана в следующем виде:
задана в следующем виде:
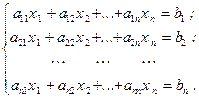 (13)
(13)
Рассмотрим известную, в принципе, из школьного курса математики, основную идею гауссова исключения неизвестных. Выразим из первого уравнения переменную 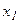 . Получим
. Получим
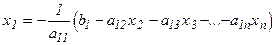 .
.
Подставим данное выражение для 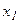 во второе и во все последующие уравнения, приведем подобные члены тем самым исключив из этих уравнений переменную
во второе и во все последующие уравнения, приведем подобные члены тем самым исключив из этих уравнений переменную 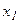 . Система примет вид
. Система примет вид

или
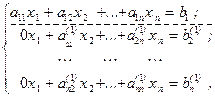
где дополнительный верхний индекс в скобках указывает, что данные коэффициенты пересчитаны в ходе выполнения указанных преобразований.
Говорят, что выполнен первый шаг гауссова исключения переменных.
По аналогии из второго уравнения преобразованной системы выразим 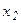 и выполним для третьего и всех последующих уравнений второй шаг – преобразования, аналогичные описанным выше. Получим систему вида
и выполним для третьего и всех последующих уравнений второй шаг – преобразования, аналогичные описанным выше. Получим систему вида
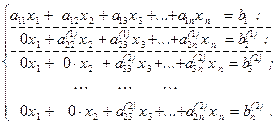
Отметим, что после выполнения каждого шага размерность подлежащей пересчету активной части матрицы уменьшается на 1.
Выполнив ровно n – 1 шаг, получим систему с матрицей коэффициентов, преобразованной к верхней треугольной форме:
 (14)
(14)
Общая формула пересчета коэффициентов при неизвестных на k -ом шаге
имеет вид
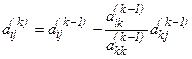 , i>k, j>k, (15)
, i>k, j>k, (15)
а формула пересчета свободных членов может быть представлена следующим образом:
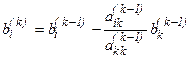 , i>k. (16)
, i>k. (16)
Очевидно, что данное выражение может быть использовано, если коэффициент 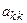 , называемый главным элементом на данном шаге, не равен нулю. Если на k -ом шаге
, называемый главным элементом на данном шаге, не равен нулю. Если на k -ом шаге 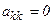 , то среди элементов матрицы
, то среди элементов матрицы 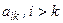 , т.е. расположенных в k -ом столбце ниже
, т.е. расположенных в k -ом столбце ниже 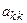 , пытаются найти не равный нулю коэффициент. Если в строке с номером i найден
, пытаются найти не равный нулю коэффициент. Если в строке с номером i найден  , то уравнения с номерами i и k меняют местами, т.е. переставляют соответствующие строки матрицы А и элементы вектора свободных членов
, то уравнения с номерами i и k меняют местами, т.е. переставляют соответствующие строки матрицы А и элементы вектора свободных членов 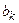 и
и 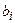 .
.
Если на k -ом шаге коэффициенты 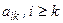 равны нулю, т.е. выбрать ненулевой главный элемент на данном шаге невозможно, то матрица А -вырождена, ее определитель равен нулю, расчет аварийно прекращают.
равны нулю, т.е. выбрать ненулевой главный элемент на данном шаге невозможно, то матрица А -вырождена, ее определитель равен нулю, расчет аварийно прекращают.
Часто выполняют обязательную перестановку уравнений в системе на каждом шаге таким образом, чтобы получить наибольший по модулю главный элемент. В результате при обработке матриц большой размерности ослабляется влияние накапливающихся ошибок округления и повышается точность решения. В этом случае говорят о методе Гаусса с выбором главного элемента.
Следует отметить, что, если приведение системы к треугольной форме выполнено в описанном порядке, то произведение n главных элементов, которые будут расположены на диагонали преобразованной матрицы, равно значению определителя матрицы А. Это свойство прямого хода гауссова исключения на практике используют для вычисления значений определителей квадратных матриц.
Второй этап – обратный ход метода Гаусса, заключается в решении полученной системы в верхней треугольной форме (14) методом обратной подстановки.
Из последнего уравнения преобразованной системы (14) находят
 .
.
Из предпоследнего уравнения преобразованной системы определяют
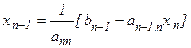
и так далее, подставляя вновь рассчитанное значение 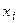 в предшествующее уравнение с номером (i – 1). Общая формула выполнения обратного хода имеет вид
в предшествующее уравнение с номером (i – 1). Общая формула выполнения обратного хода имеет вид
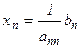
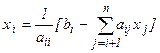 , i = n–1, n–2,...,1.
, i = n–1, n–2,...,1.
После того, как получены значения всех неизвестных полезно вычислить по формуле (9) вектор невязок и проверить точность решения. При ручном счете подобная процедура обязательна.
Задания:
1.Решить “вручную” методом Гаусса систему линейных алгебраических уравнений
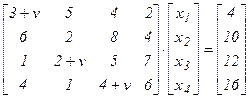
и вычислить значение определителя матрицы.
2. Выполнить решение СЛАУ на ПЭВМ.
Не нашли, что искали? Воспользуйтесь поиском: