Примеры дисперсионного анализа

Пример 1. Имеются четыре партии сырья для текстильной промышленности. Из каждой партии отобрано по пять образцов и проведены испытания на определение величины раз­рывной нагрузки. Результаты испытаний приведены в таблице.

Необходимо выяснить, существенно ли влияние различных партий сырья на величину разрывной нагрузки.

Решение

Найдем средние значения разрывной нагрузки для каждой партии:

Среднее значение разрывной нагрузки всех отобранных образцов:

(или, иначе, через групповые средние,

Вычислим суммы квадратов отклонений:

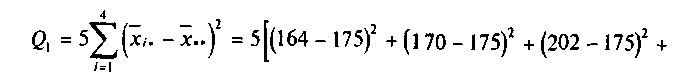
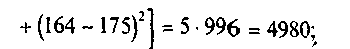
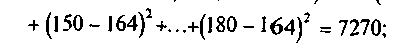
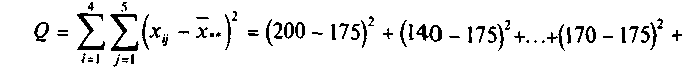
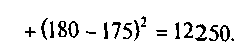
соответствующее число степеней свободы для этих сумм m-1=3; m•n-m=5 • 4-4=16; m•n-1=5•4-1 = 19. Результаты расчета сведем в таблицу:

Фактически наблюдаемое значение статистики По табл. критическое значение F-критерия Фишера—Снедекора на уровне значимости α=0,05 при k₁ =3 и k₂ =16 степенях свободы =3,24. Так как ,то нулевая гипотеза отвергается, т.е. на уровне значимости α = 0,05 (с надежностью 0,95) различие между партиями сырья оказывает существенное влияние на величину разрывной нагрузки.

Пример 2. В таблице приведены суточные привесы (г) собранных для исследования 18 поросят в зависимости от метода удержания поросят (фактор А) и качества их кормления (фактор В).

Необходимо оценить существенность (достоверность) влияния каждого фактора и их взаимодействия на суточный привес поросят.

Решение

Имеем m=3, l =2, n=2. Определим в (г) средние значения привеса Необходимо оценить существенность (достоверность) влияния каждого фактора и их взаимодействия на суточный привес поросят в ячейках:

по строкам:

по столбцам:

Общий средний привес:

Все средние значения привеса поместим в табл.

Из таблицы следует, что с увеличением количества голов в группе средний суточный привес поросят в среднем уменьшается, а при увеличении содержания протеина в корме — в среднем увеличивается. Но является ли эта тенденция достоверной или объясняется случайными причинами? Для ответа на этот вопрос по формулам вычислим необходимые суммы квадратов отклонений:

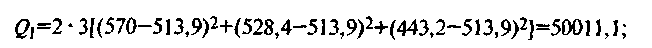
Средние квадраты находим делением полученных сумм на соответствующее им число степеней свободы m- 1 = 3-1=2, l- 1=2-1=1; (m-1)(l -1)=(3-1)(2-1)=2; mln - ml =3•2•2-3•2=12-6=6; mln-1=12-1 = 11.

Очевидно, данные факторы имеют фиксированные уровни, т.е. мы находимся в рамках модели I. Поэтому для проверки существенности влияния факторов А, В и их взаимодействия АВ необходимо найти отношения:

и сравнить их с табличными значениями соответственно :=3,88; =: =4,75; =3,88. Так как и то влияние метода содержания поросят (фактора А) и качества их кормления (фактора В) является существенным. В силу того что взаимодействие указанных факторов незначимо (на 5%-ном уровне).

Примеры дисперсионного анализа инструментами Однофакторный дисперсионный анализ, Двухфакторный дисперсионный анализ с повторениями и Двухфакторный дисперсионный анализ без повторений Пакета анализа MS Excel

Не нашли, что искали? Воспользуйтесь поиском: