
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пример решения задачи. Две концентрические проводящие сферы радиусами R1 = 6 см и R2 = 10 см несут соответственно заряды Q1 = 1 нКл и Q2 = –0,5 нКл
Две концентрические проводящие сферы радиусами R 1 = 6 см и R 2 = 10 см несут соответственно заряды Q 1 = 1 нКл и Q 2 = –0,5 нКл. Найти напряженность Е поля в точках, отстоящих от центра на расстояниях r 1 = 5 см, r 2 = 9 см, r 1 = 15 см. Построить график Е (r).
Решение. Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (рис. 2.1): области  , области
, области 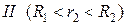 , области
, области 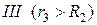 .
.
1. Для определения напряженности 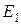 в области I проведем гауссову поверхность
в области I проведем гауссову поверхность 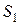 радиусом r 1 и воспользуемся теоремой Остроградского–Гаусса:
радиусом r 1 и воспользуемся теоремой Остроградского–Гаусса: 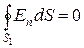 (т.к. суммарный заряд, находящийся внутри гауссовой поверхности равен нулю). Из соображений симметрии
(т.к. суммарный заряд, находящийся внутри гауссовой поверхности равен нулю). Из соображений симметрии 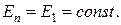 Следовательно,
Следовательно, 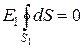 и
и 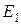 (напряженность поля в области I) во всех точках, удовлетворяющих условию
(напряженность поля в области I) во всех точках, удовлетворяющих условию  , будет равна нулю, т.е. Е 1 = 0.
, будет равна нулю, т.е. Е 1 = 0.
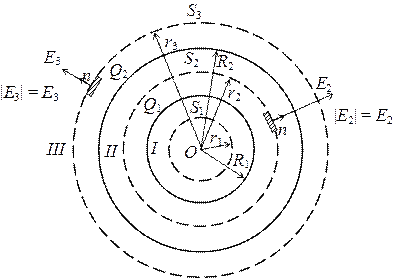
Рис. 2.1. Построение гауссовых поверхностей для расчета
напряженностей электрического поля.
2. В области II гауссову поверхность проведем радиусом r 2. В этом случае (диэлектрическую проницаемость среды будем считать равной единице (вакуум)):
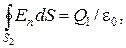 (2.18)
(2.18)
(т.к. внутри гауссовой поверхности находится только заряд 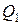 ). Из соображения симметрии
). Из соображения симметрии 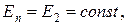 то Е можно вынести за знак интеграла:
то Е можно вынести за знак интеграла:
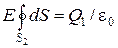 , или
, или 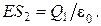 (2.19)
(2.19)
Обозначив напряженность Е для области II через 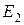 , получим
, получим
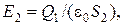 (2.20)
(2.20)
где 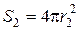 – площадь гауссовой поверхности. Тогда
– площадь гауссовой поверхности. Тогда
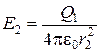 . (2.21)
. (2.21)
3. В области III гауссова поверхность проводится радиусом r 3. Обозначим напряженность Е области III через Е 3 и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен 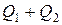 . Тогда
. Тогда
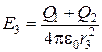 . (2.22)
. (2.22)
Заметив, что 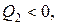 это выражение можно переписать в виде:
это выражение можно переписать в виде:
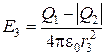 . (2.23)
. (2.23)
Убедимся в том, что правая часть равенств (2.21) и (2.23) дает единицу напряженности:
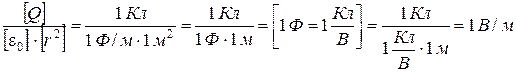 . (2.24)
. (2.24)
Выразим все величины в единицах СИ (Q 1 = 10‑9 Кл, Q 2 = –0,5×10‑9 Кл, r 1 = 0,09 м, r 2 = 0,15 м, 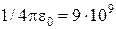 м / Ф) и произведем вычисления:
м / Ф) и произведем вычисления:
Е 2 = 1,11 кВ / м; Е 3 = 200 кВ / м.
Построим график E (r). В области  Е = 0. В области
Е = 0. В области 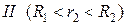
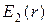 изменяется по закону
изменяется по закону 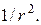 В точке
В точке 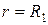 напряженность
напряженность 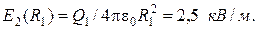 В точке
В точке 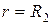 (r стремится к
(r стремится к 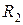 слева)
слева) 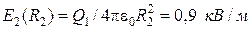 . В области
. В области 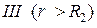
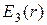 изменяется по закону
изменяется по закону 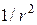 , причем в точке
, причем в точке 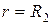 (r стремится к
(r стремится к 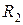 справа)
справа)  . Таким образом, функция E (r) в точках
. Таким образом, функция E (r) в точках 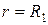 и
и 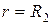 терпит разрыв.
терпит разрыв.
График зависимости E(r) представлен на рис. 2.2.
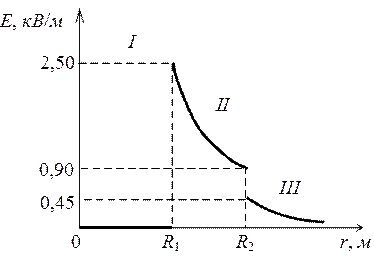
Рис. 2.2. График зависимости E(r)
Задание для самостоятельного выполнения по вариантам
Дано n проводящих фигур (сфер, цилиндров, плоскостей) или шар из изотропного диэлектрика. Каждая фигура несет заряд, характеризующийся объемной r n, поверхностной s n или линейной t n плотностью заряда. Точки А, В, С находятся на расстояниях rА, rВ, rС от центра или оси симметрии фигуры. Взаимодействие осуществляется в вакууме. Данные для решение задач приведены в табл. 2.1 и на рис. 2.3.
Фигуре с номером 1 соответствуют размеры R 1 и величины s1, r1, t1 и т.д. (рис. 2.3). Если в строке табл. 2.1 с номером вашего варианта какие-то клетки не заполнены, значит для решения вашей задачи эти данные не нужны.
1. Используя теорему Остроградского-Гаусса и принцип суперпозиции электростатических полей, найти зависимость напряженности электрического поля от расстояния Е (r) для всех областей (внутри фигуры, между фигурами и вне фигур).
2. Сделать схематический рисунок и показать направление вектора Е в каждой области.
3. Вычислить напряженность Е в точках А, В, С удаленных от центра симметрии фигур на расстояния ri.
4. Построить график зависимости Е (r) для всех областей.
Данные для выполнения задания. Таблица 2.1
| № вари-анта | Число и форма фигур | Размеры фигур, м | Поверхностная плотность заряда, нКл / м 2 | Линейная плотность заряда, нКл / м | Объемная плотность заряда, нКл / м 3 | Точечный заряд, нКл | Расстояние от центра симметрии фигуры до точек, r i м | ||||||||
| R 1 | R 2 | R 3 | s1 | s2 | s3 | t1 | t2 | t3 | r1 | q | r 1 | r 2 | r 3 | ||
| Три концентрические сферы | 0,1 | 0,2 | 0,3 | -20 | 0,05 | 0,15 | 0,4 | ||||||||
| Три концентрические сферы | 0,1 | 0,2 | 0,3 | -10 | -10 | 0,05 | 0,15 | 0,4 | |||||||
| Два коаксиальных бесконечных цилиндра | 0,1 | 0,2 | -5 | 0,05 | 0,15 | 0,3 | |||||||||
| Два коаксиальных бесконечных цилиндра | 0,1 | 0,2 | -8 | 0,05 | 0,15 | 0,3 | |||||||||
| Три коаксиальных бесконечных цилиндра | 0,1 | 0,2 | 0,3 | -10 | -20 | 0,05 | 0,15 | 0,5 | |||||||
| Три коаксиальных бесконечных цилиндра | 0,1 | 0,2 | 0,3 | -10 | 0,05 | 0,15 | 0,5 | ||||||||
| Две концентрические фигуры - шар окруженный сферой | 0,1 | 0,4 | 0,05 | 0,2 | 0,5 |
Окончание таблицы 2.1
| Две концентрические фигуры - шар окруженный сферой | 0,1 | 0,3 | -30 | -100 | 0,05 | 0,2 | 0,4 | ||||||||
| Точечный заряд в центре сферы | 0,3 | 0,1 | 0,2 | 0,4 | |||||||||||
| Точечный заряд в центре сферы | 0,2 | -10 | -20 | 0,1 | 0,3 | 0,4 | |||||||||
| Точечный заряд в центре двух концентрических сфер | 0,3 | 0,5 | -30 | -10 | 0,2 | 0,4 | 0,6 | ||||||||
| Точечный заряд в центре двух концентрических сфер | 0,2 | 0,4 | -20 | 0,1 | 0,3 | 0,5 | |||||||||
| Две бесконечные параллельные плоскости | Находятся на расст. 0,02 м друг от друга | -30 | Слева от I пл. | Между пл. | Справа от II пл. | ||||||||||
| Две бесконечные параллельные плоскости | Находятся на расст. 0,01 м друг от друга | -10 | -20 | Слева от I пл. | Между пл. | Справа от II пл. | |||||||||
| Три бесконечные параллельные плоскости | Находятся на расст. 0,02 м друг от друга | -10 | Слева от I пл. | Между I и II пл | Справа от II пл. | ||||||||||
| Три бесконечные параллельные плоскости | Находятся на расст. 0,01 м друг от друга | -10 | Слева от I пл. | Между II и III пл | Справа от III пл. |

| 
|
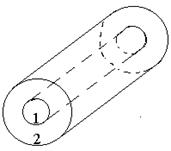
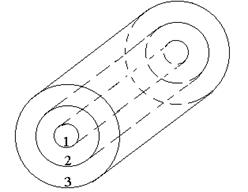
| Схема к вариантам 1, 2 | Схема к вариантам 3, 4 |
| 
|
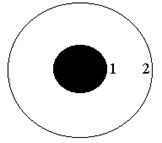
| Схема к вариантам 5, 6 | Схема к вариантам 7, 8 |
| 
|
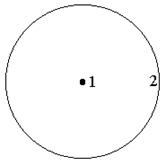
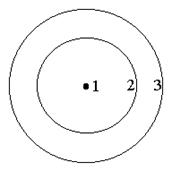
| Схема к вариантам 9, 10 | Схема к вариантам 11, 12 |

| 
|
| Схема к вариантам 13, 14 | Схема к вариантам 15, 16 |
Рис. 2.3. Схемы расположения фигур
3. Тема: Основные законы постоянного тока
Не нашли, что искали? Воспользуйтесь поиском: