ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Статистическое моделирование в логистике. Метод Монте-Карло.
Целью практического занятия является изучение численных алгоритмов статистического моделирования – «Методы Монте-Карло».
Задание 5.1. Смоделировать последовательность из 10 случайных значений времени выполнения заказа – t0, используя формулы генераторов случайных чисел для разных законов распределения.
Выполнение заказа включает три операции: 1 – приём и обработка заказа; 2 – документирование и отгрузка товара; 3 – доставка.
Время выполнения каждой операции ti случайно и определено соответствующим законом распределения f(ti). Общее время, затрачиваемое на выполнение заказа, также случайно и определяется в виде суммы:
t0 = t1 + t2+ t3. (5.1)
Параметры законов распределения следует вычислить по формулам табл.5.1 через среднее – 
и среднее квадратическое значения – 
распределения (табл.5.2.).
Таблица 5.1
Законы распределения
| Наименование (обозначение) | Плотность распределения | Параметры |
| Нормальный (Н) | 
|  , 
|
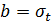
| Логарифмически нормальный (Л) | 
| 
 
|
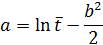
| Экспоненциальный (Э) | 
| 
|
| Равновероятный (Р) | 
| 
|
– среднее значение;  – среднее квадратическое отклонение
|
Таблица 5.2
Параметры распределения времени выполнения операция
| t1, ч | t2, ч | t3, ч | ||||||
|
|
| закон |
|
| закон |
|
| закон |
| 0,6 | 0,2 | Н | 1,8 | 0,3 | Р | 3,3 | 3,3 | Э |
Исходные последовательности псевдослучайных чисел для генерации ti выбираются из табл.5.3 – 5.4 либо моделируются встроенными функциями в Excel или пакете MathCad. Для каждого шага вычислений необходимо выбрать новое случайное число. Если для различных операция законы распределения совпадают необходимо выбрать различные последовательности псевдослучайных величин.
Таблица 5.3
Случайные равномерно распределённые в интервале [0,1] числа ξ
| 0,518 | 0,286 | 0,451 | 0,263 | 0,253 | 0,937 | 0,469 | 0,412 | 0,494 | 0,599 | |
| 0,834 | 0,157 | 0,333 | 0,160 | 0,334 | 0,924 | 0,487 | 0,675 | 0,174 | 0,972 | |
| 0,564 | 0,646 | 0,687 | 0,030 | 0,973 | 0,779 | 0,168 | 0,022 | 0,803 | 0,442 | |
| 0,903 | 0,792 | 0,415 | 0,995 | 0,663 | 0,218 | 0,538 | 0,499 | 0,995 | 0,862 | |
| 0,865 | 0,793 | 0,498 | 0,131 | 0,145 | 0,042 | 0,547 | 0,091 | 0,956 | 0,013 | |
| 0,704 | 0,181 | 0,127 | 0,517 | 0,605 | 0,079 | 0,183 | 0,456 | 0,861 | 0,042 | |
| 0,483 | 0,428 | 0,955 | 0,824 | 0,071 | 0,904 | 0,736 | 0,632 | 0,889 | 0,292 | |
| 0,109 | 0,979 | 0,457 | 0,762 | 0,893 | 0,180 | 0,112 | 0,347 | 0,596 | 0,859 | |
| 0,025 | 0,641 | 0,235 | 0,057 | 0,248 | 0,921 | 0,398 | 0,023 | 0,905 | 0,947 | |
| 0,815 | 0,563 | 0,369 | 0,446 | 0,319 | 0,791 | 0,508 | 0,160 | 0,280 | 0,207 |
Таблица 5.4
Нормально распределённые случайные числа η
| 0,428 | 0,916 | 0,892 | -1,700 | -0,031 | -0,624 | -0,704 | -0,392 | -1,613 | -0,723 | |
| -1,185 | -1,190 | -1,449 | 1,908 | 0,630 | -0,754 | 1,724 | 0,268 | -0,148 | -1,905 | |
| -0,275 | -0,409 | -0,160 | -2,485 | -1,741 | -1,377 | 0,273 | 1,661 | 0,242 | -1,370 | |
| 0,294 | 1,469 | -0,221 | 0,843 | 1,281 | -0,629 | -0,047 | -2,395 | 0,211 | -0,190 | |
| -0,003 | -1,481 | -0,474 | -0,902 | 0,628 | -1,575 | -0,803 | 0,477 | 0,125 | 1,310 | |
| 0,300 | -0,302 | 0,064 | 1,101 | -0,568 | -0,370 | -2,769 | -0,732 | 0,035 | -0,298 | |
| -1,013 | -0,219 | -0,371 | -0,108 | -1,330 | 1,253 | -1,400 | -1,772 | 0,194 | -0,120 | |
| 0,687 | -0,212 | -0,425 | 1,244 | 1,497 | -1,340 | 0,837 | -0,696 | -0,284 | -0,110 | |
| -1,121 | 0,251 | -2,742 | -1,394 | -0,742 | -0,752 | -0,375 | -0,473 | 1,051 | -1,073 | |
| 0,164 | 0,021 | 0,316 | -1,227 | 0,186 | 0,439 | -0,329 | 1,012 | 0,151 | -0,014 |
Формулы генераторов случайных величин (СВ) для различных законов распределения представлены в табл.5.5.
Таблица 5.5
Генераторы СВ
| Закон распределения | Плотность распределения | Генератор СВ |
| Равновероятный |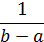 
| 
|
| Экспоненциальный |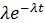 
| 
|
| Нормальный | 
| 
η – нормально распределённая нормированная СВ
|
| Логарифмически нормальный |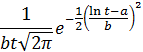 
| 
|
| Релея | 
| 
|
| Вейбулла | 
| 
|
Порядок выполнения задания:
1. Для моделирования случайных величин (табл.5.5) необходимо выбрать одну последовательность нормально распределённой случайной величин η и 2 последовательности равномерно распределённых величины ξ.
2. Для равновероятного закона распределения выберем последовательность «12» (где 1 – номер строки, а 2 – номер столбца первого элемента); для экспоненциального – последовательность «90» из табл.5.3; для нормального закона распределения последовательность «41» из табл.5.4.
3. Параметры для моделирования нормального закона (табл.5.1)
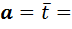0.6; 
0.2.
4. Параметры для моделирования равновероятного закона:
5. Параметры для моделирования экспоненциального закона:
0.30.
6. Результаты статистического моделирования ti представлены в табл.5.6.
Таблица 5.6
Результаты моделирования
| Величина | ||||||||||
| η | -1,48 | -0,47 | -0,90 | 0,63 | -1,58 | -0,80 | 0,48 | 0,13 | 1,31 | 0,30 |
| t1 | 0,30 | 0,51 | 0,42 | 0,73 | 0,29 | 0,44 | 0,70 | 0,63 | 0,86 | 0,66 |
| ξ1 | 0,33 | 0,16 | 0,33 | 0,92 | 0,49 | 0,68 | 0,17 | 0,97 | 0,56 | 0,65 |
| t2 | 1,63 | 1,45 | 1,63 | 2,23 | 1,79 | 1,98 | 1,47 | 2,28 | 1,87 | 1,95 |
| ξ2 | 0,82 | 0,56 | 0,37 | 0,45 | 0,32 | 0,79 | 0,51 | 0,16 | 0,28 | 0,21 |
| t3 | 0,68 | 1,90 | 3,29 | 2,66 | 3,77 | 0,77 | 2,24 | 6,05 | 4,20 | 5,20 |
| t0 | 2,61 | 3,85 | 5,34 | 5,62 | 5,84 | 3,19 | 4,40 | 8,95 | 6,93 | 7,81 |
Задание для самостоятельного решения:
Задание 5.2. Смоделировать время доставки товаров со склада в Москве на склад магазина в Санкт-Петербурге. Выполнение заказа включает следующие операции: t1 – подготовка товара под заказ (документирование, комплектация и пр.); t2 – подготовка к транспортировке и погрузка; t3 –транспортировка; t4 – приём товара, разгрузка и оформление документов. Время транспортировки определяется через среднюю скорость автопоезда на трассе 
при расстоянии перевозки L=700 км. Исходные данные для моделирования представлены в табл.5.7
Таблица 5.7
Параметры распределения времени выполнения операция
Не нашли, что искали? Воспользуйтесь поиском: