Аксиома затвердевания

Твёрдое тело называется свободным, если оно может перемещаться в любом направлении пространства.

Тела, ограничивающие свободу перемещения данного тела и делающие его несвободным, называются связями. В связях под действием приложенных к телу сил (активных сил) возникают усилия, называемые реакциями связей.

Согласно принципу освобождаемости от связей, несвободное твёрдое тело можно рассматривать как свободное, если освободиться от связей, а их действие на тело заменить реакциями связей.

Рассмотрим наиболее часто встречаемые в задачах статики связи и возникающие в них реакции связей.

1. Гладкая (идеальная) поверхность (поверхность без трения)

Реакция такой поверхности (рис. 5а) направлена по общей нормали к соприкасающимся поверхностям.

Если одна из поверхностей обращается в точку (рис. 5б), то реакция направлена по нормали ко второй поверхности. Отсюда следует, что реакция цилиндрической подвижной (катковой) опоры А (рис. 6а) направлена по нормали к опорной поверхности. Иногда в задачах катковую опору изображают в виде "салазок" (рис. 6б).

2. Гибкая нить

Реакция гибкой нити направлена по нити к точке подвеса (рис. 7).

3. Цилиндрический шарнир

Эта связь не препятствует повороту тела в плоскости Оху, перпендикулярной оси шарнира (рис. 8а), но препятствует радиальному перемещению тела. В задачах обозначается, как показано на рис. 8б.

Реакция цилиндрического шарнира может иметь любое направление в плоскости, и неизвестными являются модуль и угол 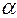, характеризующий направление её линии действия. Обычно вместо и 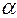рассматривают и – составляющие реакции по осям координат.

4. Сферический (пространственный) шарнир

Сферический шарнир не препятствует повороту тела в пространстве (рис. 9а), в задачах обозначается так же, как и цилиндрический шарнир (рис. 9б).

Реакция сферического шарнира может иметь любое направление в пространстве, и неизвестными являются её модуль R и два утла 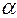и 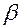её наклона к осям Ох, Оу. Обычно вместо этих неизвестных вводят три составляющие , и реакции по координатным осям.

5. Подпятник

В подпятнике (рис. 10), как и в сферическом шарнире, неизвестными являются три составляющие реакции по осям координат: , и .

6. Невесомый стержень с шарнирами на концах

Реакция такого стержня СВ (рис. 11а) направлена по стержню. Причём, если реакции стержня на узлы направлены к узлам, значит, со стороны узлов действуют сжимающие силы 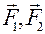– стержень работает на сжатие (рис. 11б), если реакции направлены от узлов – на растяжение (рис. 11в).

7. Плоская заделка

Если действующие на балку АВ (рис. 12) силы расположены в плоскости балки (плоскость чертежа), в этом случае А – плоская заделка.

В плоской заделке – три неизвестных: две составляющие , реакции на оси координат и пара с моментом .

8. Пространственная заделка

Если действующие на балку АВ силы имеют произвольное направление в пространстве, в этом случае А – пространственная заделка (рис. 13). В пространственной заделке шесть неизвестных: три составляющие , и реакции на оси координат и три пары относительно координатных осей с моментами .

9. Скользящая опора

Для бруса AB связь A – скользящая опора (рис. 14). В опоре A две неизвестных: реакция и момент .

Не нашли, что искали? Воспользуйтесь поиском: