Примеры решения задач на равновесие тел

Под действием системы сходящихся сил

Для решения задач статики на равновесие материальных объектов под действием любых систем сил можно рекомендовать следующий порядок:

1. Выбрать объект равновесия.

2. Используя аксиому отбрасывания связей, выделить объект равновесия, к которому приложены активные силы и реакции связей.

3. Сделать заключение о действующей на объект системе сил и составить соответствующие уравнения равновесия.

Пример 1

Балка АВ (рис. 19а) концом А крепится к основанию цилиндрическим шарниром, конец В – цилиндрическая подвижная (катковая) опора. В середине балки АВ под углом 45° к её оси действует сила . Определить реакции опор.

Решение

1. Объект равновесия – балка АВ.

2. Активные силы – .

Реакции связей: направлена перпендикулярно опорной поверхности, линия действия реакции , согласно теореме о трёх силах, должна проходить через точку О.

3. Балка находится в равновесии под действием плоской системы сходящихся сил.

Для такой системы необходимо выполнение условий равновесия (1.5). Однако если объект находится в равновесии под действием плоской системы трёх сходящихся сил, то вместо составления уравнений равновесия (1.5) задачу обычно рекомендуют решать графо-аналитическим способом.

Геометрическое условие равновесия

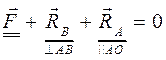. (1.6)

В равенстве (1.6) вектор подчеркнут двумя чертами, так как известны его модуль и направление его линии действия, векторы и – одной чертой, ибо известны только направления их линий действия (направление указано в 1.6).

Равенство (1.6) содержит два неизвестных – модули и . Векторные равенства, содержащие два неизвестных, можно решать либо аналитически (путем проектирования их на две оси), либо графически (путем построения многоугольника сил). Решаем равенство (1.6) графически. Откладываем вектор заданной силы (рис. 20). Из конца вектора проводим линию, параллельную вектору реакции , а из начала – линию, параллельную . Из геометрического условия равновесия системы сходящихся сил следует, что и должны быть направлены так, чтобы стрелки, указывающие направление векторов, были направлены по контуру треугольника сил. Силовой треугольник на (рис. 20) даёт действительное направление реакций и . Следовательно, силы и (рис. 19б) направлены правильно.

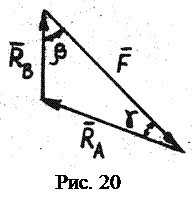Построением силового треугольника (рис. 20) завершается графическое решение равенства (1.6). Аналитический этап в графоаналитическом способе заключается в геометрическом решении треугольника сил. Треугольник сил (рис. 20) и треугольник ОАС на рис. 19б подобны (как треугольники с параллельными сторонами). Из подобия треугольников следует

. (1.7)

В треугольнике АОС

Из выражения (1.7) следует, что

Пример 2

Груз Е (рис. 21) весом Р поднимается лебёдкой D при помощи троса DАЕ, перекинутого через блок А. Пренебрегая трением троса о блок, найти реакции невесомых стержней АВ и АС в зависимости от угла a. Определить, при каком угле a усилие стержня АВ равно нулю.

Решение

1. Объект равновесия – узел А.

2. Активные силы: .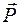

Реакции связей: 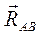, (направлены по стержням), . Так как А – идеальный блок, то Т = Р. Учитывая, что на узел А действует плоская система сходящихся сил и общее число действующих сил больше трёх, составляем два уравнения равновесия (1.5):

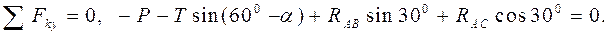
Из уравнений (1.8) с учётом того, что Т = Р, находим

(1.9)

Из первого выражения (1.9) следует, что при 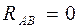получаем

.

Таким образом, при усилие стержня АВ равно нулю.

Пример 3

Определить усилия (рис. 22) невесомых стержней АВ, АС, АD, которые идеальным шарниром скреплены в точке А и идеальными шарнирами В, С, D крепятся к вертикальной стене. К узлу А подвешен груз Е весом Р.

Решение

1. Объект равновесия – узел А.

2. Активные силы: .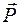

Реакции связей: , , .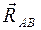

3. На узел А действует пространственная система сходящихся сил.

Составляем три уравнения равновесия (1.4) для пространственной системы сходящихся сил:

(1.10)

Из выражений (1.10) получаем

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется связью? В чём заключается аксиома освобождаемости от связей?

2. Перечислите основные виды связей и возникающие в них реакции.

3. Что называется равнодействующей и главным вектором системы сил?

4. Как определяется направление равнодействующей системы сходящихся сил при построении силового многоугольника?

5. В чём выражается геометрическое условие равновесия плоской и пространственной систем сходящихся сил?

6. Каковы уравнения равновесия плоской и пространственной систем сходящихся сил?

7. Как читается теорема о равновесии тела под действием систем трёх непараллельных сил?

Не нашли, что искали? Воспользуйтесь поиском: