Частный случай приведения плоской системы сил

К одному центру

При приведении плоской произвольной системы сил к произвольному центру О получаем одну силу , равную геометрической сумме сил системы и называемую главным вектором системы сил

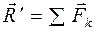, (2.18)

и одну пару , называемую главным моментом системы сил относительно центра приведения О. Учитывая, что при параллельном переносе сил моменты присоединяемых согласно лемме Пуансо пар для плоской системы сил находятся в плоскости действия сил системы, а пары на плоскости суммируются алгебраически, получаем, что для плоской системы сил главный момент относительно центра О равен алгебраической сумме моментов сил системы относительно центра О:

(2.19)

Модуль главного вектора плоской системы сил определяется по его двум проекциям на оси координат

. (2.20)

Тогда ,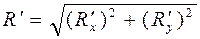

.

Частные случаи приведения плоской системы сил к одному центру:

1. 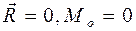– система сил находится в равновесии.

2. – система сил приводится к равнодействующей, линия действия которой проходит через центр приведения О.

3. – система приводится к паре сил, момент которой не зависит от выбора центра приведения О.

4. . Учитывая, что для плоской системы сил вектор главного момента относительно любого центра приведения О всегда перпендикулярен , т.е. , этот случай приведения плоской системы сил аналогичен случаю 4 приведения пространственной системы сил (), значит, в этом случае плоская система сил приводится к равнодействующей.

Можно сделать вывод, что плоская произвольная система сил всегда приводится к равнодействующей, если не находится в равновесии (случай 1) и не приводится к одной паре (случай 3).

Не нашли, что искали? Воспользуйтесь поиском: