Многочлены Жегалкина.

Многочлен Жегалкина – многочлен над полем GF(2), в котором в качестве умножения используется конъюнкция, а в качестве сложения – сложение по модулю 2.

Многочлен Жегалкина представляет собой сумму по модулю два произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально многочлен Жегалкина можно представить в виде

Любую булеву функцию можно выразить через многочлен Жегалкина.

На самом деле, вот это вот куда проще, чем он объяснял.

Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:

· Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от 000…00 до 111…11. · Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности. · Ячейка в каждом последующем столбце получается путём суммирования по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже. · Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности. · Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке 111 соответствует член ABC, ячейке 101 — член AC, ячейке 010 — член B, ячейке 000 — член 1 и т. д. · Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина.

Основные понятия и определения комбинаторики.

- число перестановок (упорядочивание)

- число перемещений (число размещений)

- число сочетаний (без учета порядка)

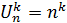- число сочетаний с возвращениями с учетом порядка

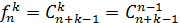- число сочетаний с возвращениями без учета порядка (число сочетаний с повторениями)

Не нашли, что искали? Воспользуйтесь поиском: