Объем пирамиды (вывод). Объем усеченной пирамиды. Пусть SABC – треугольная пирамида с вершиной S и основанием ABC

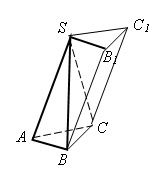
Пусть SABC – треугольная пирамида с вершиной S и основанием ABC. Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой. Эта призма составлена из трех пирамид: данной пирамиды SABC и еще двух треугольных пирамид SCC₁B₁ и SCBB₁.
У второй и третьей пирамид равные основания - ΔCC₁B₁ и ΔB₁BC и общая высота, проведенная из вершины S. Поэтому у них равные объемы.
У первой и третьей пирамид тоже равные основания - ΔSAB и ΔBB₁S и совпадающие высоты, проведенные из вершины C. Поэтому у них тоже равные объемы.
Значит, все три пирамиды имеют один и тот же объем. Так как сумма объемов равна объему призмы, то объемы пирамид равны .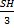
Объем любой треугольной пирамиды равен одной трети произведения площади основания на высоту:

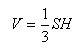
Есть усеченная пирамида с площадями оснований S1 и S2 (S1>S2) и высотой h.

Тогда объем усеченной пирамиды равен:

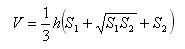
Не нашли, что искали? Воспользуйтесь поиском: