Обернена пропорційність, її властивості та графік. Методика навчання розв’язування задач на пропорційний поділ.

Обернена пропорційність- функція, задана формулою y=k/х, де k?0 Число k називають коефіцієнтом оберненої пропорційності.

Властивості функції y=k/x:

1. Область визначення- множина всіх дійсних чисел крім нуля

2. y=k/x- непарна функція

3. Якщо k>0, то функція убуває на проміжку (0;+() і на проміжку (-(;0). Якщо k<0, то функція зростає на проміжку (-(;0) і на проміжку (0;+().

Графіком функції є гіпербола.

5)Функція y=x2

Властивості функції y=x2:

1. Область визначення- вся числова пряма

2. y=x2 - парна функція

3. На проміжку [0;+() функція зростає

4. На проміжку (-(;0] функція убуває

Графіком функції є парабола.

Методика

Задача на пропорційне ділення та задачі на знаходження невідомих за двома різницями вивчається у 4 класі.

Дана методика побудована на єдиному плані, в якому проілюстровані наступні аспекти:

- для усвідомлення учнями зв’язку задач на знаходження 4-го пропорційного і задачі на пропорційне ділення здійснюється перетворення задачі відомого виду в задачу нового виду;

дослідження задачі реалізується шляхом заміни величини або числових даних задач і визначення впливу цих змін на план розвязку задачі. Безпосереднє ознайомлення із задачами на знаходження невідомого за двома різницями проводиться на основі розв'язування трьох задач, поданих нижче.

Задача 1. Перший покупець купив 2 м тканини і заплатив 18 грн. Скільки гривень коштує 1 м тканини?

Задача 2. Перший покупець купив 5 м тканини, а другий — 3 м такої самої тканини. Перший покупець заплатив на 18 грн. більше, ніж другий. Скільки гривень коштує 1 м тканини?

Задача 3. Перший покупець купив 5 м тканини, а другий ~ 3 м такої самої тканини. Перший покупець заплатив на 18 грн. більше, ніж: другий. Скільки гривень заплатив другий покупець?

Ознайомлюючи учнів із задачею на знаходження величини за двома різницями, вчитель прочитав задачу такого змісту: "З першої ділянки зібрали 6 кошиків моркви, а з другої — 4 таких самих кошики. З першої ділянки зібрали на 40 кг моркви більше, ніж з другої. Скільки кілограмів моркви зібрали з кожної ділянки окремо?" — і запропонував учням розглянути малюнок (мал. 131).

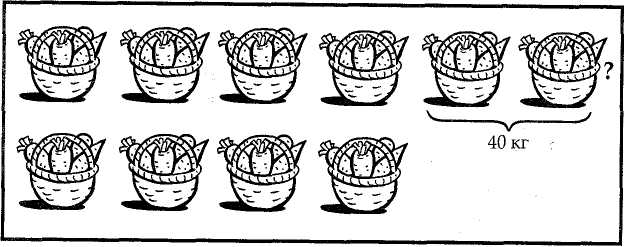
— Чому з першої ділянки зібрали на 40 кг моркви більше, ніж з другої?

— Маса скількох кошиків моркви, зібраної з першої ділянки, така сама, як і маса моркви, зібраної з другої ділянки? "

— Маса скількох кошиків моркви дорівнює 40 кг?

— Складіть план розв'язування задачі.

-

Кратні, спільні кратні, найменше спільне кратне двох і більше чисел. Методика вивчення математичних виразів при викладанні освітньої галузі «Математика». Правила порядку виконання дій.

Якщо відомо,що число а є кратним числе в, тобто а в, то це еквівалентно, а (а=b q), де q множині натуральних чисел. Нуль є кратним будь-якого числа. Спільним кратним натуральних чисел а і в наз. натуральне число кратне кожному з даних чисел(дане число має націло ділитися на дані числа). Наймене спільне кратне натуральних чисел наз. найменше число з усіх спільних даних чисел.Щоб знайти НСК за їх канонічним розкладом необхідно і достатньо знайти канонічний розклад даних чисел і обчислити добуток всіх множників в максимальних степенях.

Методика

Поняття про числовий вираз у молодших школярів формують у тісному зв'язку з вивченням арифметичних дій. Робота над виразами проводиться в такій послідовності:

а) формування уявлень про найпростіші вирази (сума та різниця двох чисел) та введення виразів на дві дії (7 + 2 + 3; 12 — 3 — 4; 9 + 4 — 2);

б) вирази на дві дії першого ступеня із застосуванням дужок (10 — (4 + 3); 17-(10-3); 5+ (4-1));

в) вирази на дві дії першого і другого ступенів, знаходження числових значень яких виконується в порядку наступності дій (12: 3 + 8; 2 • 4 — 5; 6:2- 8);

г) вирази на дві дії першого і другого ступенів, знаходження числових значень яких спирається на правила порядку виконання арифметичних дій (20 - 16:2; 24: (3 • 2)), вирази на три і більше дій (9 • 8 + 9 • 3; 4038 • 97 - 2460: 60).

Розкриємо суть роботи на кожному з цих етапів.

Перший етап припадає на час вивчення додавання і віднімання в межах 10 та складання таблиць додавання і віднімання з переходом через десяток. У цей період знаки "+" і "-" у прикладах виду 2 + 3; 5 - 1 виступають лише як коротке позначення слів "додати" і "відняти". Це відтворюється в процесі читання: до числа два додати три, буде п 'ять. У робочому плані вводять термін "приклад". Такі записи, як 2 + 1 = 3; 3 + 2 = 5, називають прикладами на додавання. Згодом діти дізнаються, що, додаючи кілька одиниць, збільшуємо число на стільки ж одиниць, а віднімаючи — зменшуємо його на стільки ж одиниць. Вводять також назви компонентів і результатів дій,назви знаків дій "плюс" і "мінус". У ході роботи вчитель "непомітно" вводить термін "вираз".

Якщо учні не розуміють завдання, то вчитель змінює формулювання, доповнює його. Словосполучення "значення виразу" на першому етапі не використовується.

На другому етапі (під час запровадження дужок) розкривається інше значення знаків дій — знак дії визначає вираз: 5 + 2 — це сума чисел 5 і 2; 9 — 3 — це різниця чисел 9 і 3. Спираючись на знання дітей про назви чисел при діях додавання і віднімання, вчитель пояснює, що запис, який скла­дається з двох чисел, сполучених знаком "плюс", називається так само, як і результат дії додавання, тобто сумою, а запис, який складається з двох чисел, сполучених знаком "мінус", називається так само, як результат дії відні­мання, тобто різницею.

Наприклад, 27 + 1 = 28 18 - 6 = 12

сума сума різниця різниця

Щоб учні засвоїли нові значення термінів "сума" і "різниця" як назви виразів, їм слід пропонувати вправи виду: обчисліть суму (різницю) чисел 10 і 6; запишіть суму (різницю) чисел 8 і 7 (обчислювати результат не треба); порівняйте суми (різниці) чисел 12 і 7 та 12 і 5; прочитайте той вираз, який є сумою; замініть число сумою чисел. Діти мають зрозуміти, що при обчисленні суми (різниці) виконується вказана дія, а при записі суми (різниці) отримуємо два числа, сполучених знаком "плюс" ("мінус").

Ознайомлення учнів з термінами "числовий вираз" та "значення виразу" подається за допомогою розповіді.

Учитель повідомляє дітям, що записи виду 25 + 3; 60 — 20; 10+4 — 8; 16-(8 - 5) називають числовими виразами. Якщо в цих числових виразах виконати зазначені дії, то отримаємо значення виразів. Наприклад: 25 + 3 = 28. Інакше кажучи, значення виразу 25 + 3 дорівнює 28, або сума чисел 25 і З дорівнює 28.

Третій етап припадає на початок ознайомлення з діями множення та ділення і триває до запровадження правил порядку виконання арифметичних дій. Діти повинні засвоїти назви компонентів і результатів дій множення та ділення, а також закріпити, що терміни "сума", "різниця", "добуток" і "частка" означають не тільки результати відповідних дій, а й самі вирази цих дій. Засвоєння учнями термінології відбувається в процесі виконання системи відповідних вправ.

На четвертому етапі розглядається правило обчислення значень виразів, що містять дії різних ступенів (у довільному порядку), подаються формулю­вання всіх правил порядку виконання дій. Ознайомлення з цим матеріалом виконують прямим повідомленням та читанням правил за підручником.

Робота над виразами проводиться у такій послідовності:

1. при обчисленні значення виразу виконуємо дії, які є в дужках.2.Якщо в прикладі дужок немає, то виконуємо дії ІІступ.(множ.діл.), а потім дії І ст..(додав. відн.)3.Якщо дії даного ступеня записані без дужок, то виконуємо обчислення в порядку запису в прикладах.

Не нашли, что искали? Воспользуйтесь поиском: