
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Квадратична функція і її властивості та графік. Ознайомлення учнів з часом та його одиницями при вивченні змістової лінії «Величини та одиниці вимірювання величин».
Квадратичною функцією називається функція, яку можна задати формулою виду  , де x — незалежна змінна, a, b, c — довільні числа, причому
, де x — незалежна змінна, a, b, c — довільні числа, причому  .
.
Графіки функцій  і
і  — рівні параболи, які можна сумістити паралельним перенесенням.
— рівні параболи, які можна сумістити паралельним перенесенням.
Будь-яку функцію  можна представити у вигляді
можна представити у вигляді  , де m і
, де m і  , n — деякі дійсні числа. А це означає, що графік функції
, n — деякі дійсні числа. А це означає, що графік функції  можна дістати за допомогою двох паралельних перенесень графіка функції
можна дістати за допомогою двох паралельних перенесень графіка функції 
Отже, щоб дістати графік функції 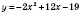 , треба зробити з графіком функції
, треба зробити з графіком функції  такі перетворення:
такі перетворення:
1) відобразити симетрично осі Ox;
2) зробити паралельне перенесення на три одиничних відрізка в напрямі осі Ox;
3) зробити паралельне перенесення на один одиничний відрізок униз.
Зробимо всі ці перетворення й отримаємо графік функції 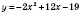 :
:

При побудові параболи користуються такими загальними формулами та властивостями квадратичної функції.
1. Координати вершини параболи  :
:
x в=  ; y в=
; y в=  або y в= y (x в).
або y в= y (x в).
Зручніше знаходити ординату вершини як значення функції, що відповідає значенню аргументу x = x в.
2. Точки перетину параболи з осями координат є такими:
Абсциса точки перетину параболи з віссю Oy дорівнює 0, тоді  ,
,  .
.
Ордината точок перетину параболи з віссю Ox дорівнює 0, тоді, щоб знайти абсциси цих точок, треба розв’язати квадратне рівняння  .
.
Якщо це рівняння має два різних корені  і
і  , графік перетинає вісь Ox у точках
, графік перетинає вісь Ox у точках  ,
,  .
.
Якщо це рівняння має один корінь (тобто 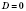 ), то цей корінь
), то цей корінь  .
.
Це означає, що вершина параболи лежить на осі Ox і має координати 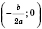 .
.
Якщо це рівняння не має коренів  , парабола не перетинає вісь Ox.
, парабола не перетинає вісь Ox.
3. Напрям віток параболи залежить від знака коефіцієнта a.
Якщо  , вітки параболи напрямлені вгору.
, вітки параболи напрямлені вгору.
Якщо  , вітки параболи напрямлені вниз.
, вітки параболи напрямлені вниз.
4. Парабола є симетричною відносно прямої  .
.
На рисунках, поданих нижче, наведені ескізи розміщення параболи на координатній площині в деяких випадках.
Методика
В результаті вивчення теми «час та його властивості» в учнів мають бути сформовані певні вміння і уявлення про такі одиниці вимірювання часу як: століття, рік, місяць, тиждень, доба, година, хвилина, секунда. Вони повинні знати таблицю мір часу, порядок днів тижня і місяців у році, вміти перетворювати іменовані числа, визначати час за годинником.
Конкретні уявлення про добу, годину й хвилину формується в учнів на основі власних спостережень та їх прктичної діяльності.
Виконуючи практичні вправи з моделями годинника, учні вчаться визначати час за годинником. З допомогою моделі годинника читають по-різному час розміщуючи годинникову і хвилинну стрілки за вказівками вчителя, розв’язуючи задачі на час.
Почати роботу з формування в учнів уявлень про рік і місяць доцільно з повідомлення про те, що одиниці вимірювання часу пов’язані з рухом планети Землі навколо Сонця, рухом Місяця навколо Землі.
Вивчивши та під час вивчення з учнями одиниці вимірювання часу систематизуються у вигляді таблиці, яку складають вони самі.
| Одиниця часу | Позначається скорочено | Співвідношення між одиницями часу |
| Секунда | с | 1 хв = 60 с |
| Хвилина | хв | 1 год = 60 хв |
| Година | год | 1 доба = 24 год |
| Доба | доба | 1 доба = 24 год |
| Місяць | міс | 1 міс. = 30 обо 31 день (у лютому 28 або 2яф днів) |
| Рік | р. | 1звичайний рік – 365 діб 1 високосний рік – 366 діб |
| Століття | ст. | 1 століття -100 років |
Бінарні відношення на множині. Властивості бінарних відношень. Методика ознайомлення молодших школярів з масою та її одиницями при вивченні змістової лінії «Величини та одиниці вимірювання величин».
Якщо множина відправлення і множина прибуття збігаються, то такі відповідності називаються відношеннями.
Бінарними відношеннями називають підмножину декартового добутку, який називають декартовим квадратом
Поняття відношень між множинами відносяться до числа фундаментальних понять математики. І не тільки тому, що воно лежить в основі визначення таких важливих понять математики, як функції і відображення, але й тому, що в будь-якій науці вивчаються не тільки самі об'єкти, але і зв'язки між ними.
Розглянемо бінарне відношення, тобто відношення між двома елементами однієї або різних множин.
Спочатку розглянемо приклад бінарного відношення між елементами двох множин А і В.
А = {Сашко, Борис, Володя, Галя, Таня, Оленка}
В = {футбол, волейбол, плавання, гімнастика, теніс}
За допомогою слів „займатися яким-небудь видом спорту” між елементами цих множин встановлено зв'язок, або, як говорять в математиці, відношення. В результаті ми одержали третю множину Р
Р = {(Сашко, волейбол), (Сашко, теніс), (Борис, футбол),
(Володя, плавання), (Галя, волейбол), (Оленка, теніс)}
Р А х В
Найважливіші з них мають певні назви і позначення:
відношення рівності (=); відношення перпендикулярності (); відношення паралельності (¦); відношення подільності; відношення включення (); відношення конгруентності (); відношення подібності (~).
Бінарне відношення (бінарне відношення на множині) — в математиці окремий випадок відношення на множині, яке встановлюється між двома елементами множини.
Кажуть також, що елементи a,b ∈ M знаходяться у бінарному відношенні R (часто записують у вигляді a R b), якщо впорядкована пара (a,b) ∈ R. Отже, R є підмножиною декартового квадрата: R ⊆ M×M.
Іноді розрізняють поняття бінарного відношення на множині та бінарного відношення між множинами, яке в цій енциклопедії називається відповідністю між множинами.
Приклади бінарних відношень на множині натуральних чисел  :R1 — відношення
:R1 — відношення  («менше або дорівнює»), тоді 4 R1 9 та 5 R1 5.;R2 — відношення «ділиться на», тоді 4 R2 2, 49 R2 7, m R2 1 для будь-якого натурального m.;R3 — відношення «є взаємно простими», тоді 15 R3 8, 366 R3 121, 1001 R3 612.;R4 — відношення «складаються з однакових цифр», тоді 127 R4 721, 230 R4 302, 3231 R4 3213311.
(«менше або дорівнює»), тоді 4 R1 9 та 5 R1 5.;R2 — відношення «ділиться на», тоді 4 R2 2, 49 R2 7, m R2 1 для будь-якого натурального m.;R3 — відношення «є взаємно простими», тоді 15 R3 8, 366 R3 121, 1001 R3 612.;R4 — відношення «складаються з однакових цифр», тоді 127 R4 721, 230 R4 302, 3231 R4 3213311.
Операції з відношення Оскільки відношення на M є також множинами, то над ними дозволені теоретико-множинні операції. Наприклад:перетином бінарних відношень "більше або дорівнює" і "менше або дорівнює" є відношення "дорівнює",об’єднанням відношень "менше" і "більше" є відношення "не дорівнює",доповненням відношення "ділиться на" є відношення "не ділиться на" тощо.
Методика
Уявлення про масу можна розкрити спираючись на дії з предметами.
Діти встановлюють, що один предмет важчий ніж другий. Відповідні ситуації можна створити на уроці під час ознайомлення учнів з терезами та їх будовою.
Вчитель пропонує порівняти учням два будь-які предмети, що мало відрізняються за масою (2 книжки).
Після цього потрібно підвести учнів до того що необхідно мати одиницю вимірювання маси. Виклавши на стіл гирю 1 кг маси і два предмети, маса одного з них трохи більша від 1 кілограма, і менша. Вчитель питає учнів, маса якого предмета більша? А якого менша? Як розв’язати цю задачу за допомогою гирі?
Учні за допомогою гир вимірюють масу різних предметів.
У 3 класі школярі ознайомлюються з новою одиницею маси – грамом. Конкретне уявлення про грам діти отримають під час безпосереднього споглядання та користування набором важків.
Щоб створити в учнів конкретно уявлення про такі одиниці маси як: центнер і тонна, потрібно навести приклади маси різних предметів.
25. Площа фігури та її властивості. Способи вимірювання площ. Методика формування уявлень про площу фігури та одиниці площі при вивченні змістової лінії «Геометричні фігури. Властивості геометричних фігур»
Площа — величина, що визначає розмір поверхні, одна з основних властивостей геометричних фігур. Історично, обчислення площі називалосяквадратурою. Фігура, що має площу, називається квадрованою. Площу нескладних геометричних фігур визначають, підраховуючи кількість одиничних квадратів, якими фігури можна покрити. Площу заведено позначати великою латинською літерою S.
Існує декілька способів визначення площі: • аналітичний, коли площу вираховують за результатами вимірювань ліній ікутів, або їх функцій координат вершин ділянок;• графічний, коли площу визначають за результатами вимірювань ліній ікутів, чи координат на планах, картах або з допомогою палеток;• механічний, коли площі визначають на плані за допомогою спеціальнихприладів - планіметрів, картометрів тощо.Методика
Методика вивчення геометричних фігур включає: актуалізацію опорних знань; вивчення властивостей фігур із залученням досвіду дитини, з опорою на навколишні предмети; широке використання різних видів наочності; виконання практичних робіт; розв'язування системи вправ, диференційованих за складністю.
У початкових класах геометричні фігури розглядаються лише за формою і розмірами без аналізу їх властивостей. Особливу роль при вивченні геометричних фігур у 1 – 4 класах відіграє практична діяльність учнів. Засвоєння матеріалу покращується, якщо вони відтворюють геометричні форми в процесі моделювання, конструювання, креслення, вирізання, малювання, утворення фігур шляхом перегинання листка паперу, розпізнавання фігур на кресленнях і в навколишній дійсності. Таким чином, після закінчення 4 класу в учнів накопичується значний обсяг знань і уявлень про геометричні фігури, які в наступних класах узагальнюються і систематизуються. Вивчення геометричного матеріалу супроводжується використанням наочності. На кожному етапі навчання і для кожного рівня навчальної діяльності учнів роль і місце засобів унаочнення різні. При вивченні геометричних фігур основними засобами наочності для учнів 1 – 4 класів є спочатку конкретний предмет, який замінює геометрична матеріальна модель, а потім геометричний рисунок.
Не нашли, что искали? Воспользуйтесь поиском: