Основные свойства определителей. Сформулируем и докажем основные свойства определителей 2-го и 3-го порядка (доказательство проведем для определителей 3-го порядка).

Сформулируем и докажем основные свойства определителей 2-го и 3-го порядка (доказательство проведем для определителей 3-го порядка).

Свойство 1. Определитель не изменяется при транспонировании, т.е.

Доказательство.

=

Замечание. Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы.

Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.

.

Доказательство.

Свойство 3. Определитель, имеющий нулевую строку, равен 0.

Доказательство этого свойства следует из свойства 2 при k = 0.

Свойство 4. Определитель, имеющий две равные строки, равен 0.

Доказательство.

Свойство 5. Определитель, две строки которого пропорциональны, равен 0.

Доказательство следует из свойств 2 и 4.

Свойство 6. При перестановке двух строк определителя он умножается на –1.

Доказательство.

Свойство 7.

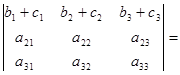
Доказательство этого свойства можно провести самостоятельно, сравнив значения левой и правой частей равенства, найденные с помощью определения 1.5.

Свойство 8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

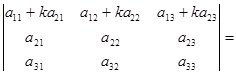
Доказательство следует из свойств 7 и 5.

Билет 3.

Обратная матрица.

Ответ: Определение 3.7. Квадратная матрица А называется вырожденной, если , и невырожденной, если .

Определение 3.8. Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается .

Рассмотрим условие существования матрицы, обратной к данной, и способ ее вычисления.

Теорема 3.2. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.

Доказательство.

1) Необходимость: так как то (теорема 3.1), поэтому

2) Достаточность: зададим матрицу в следующем виде:

.

Тогда любой элемент произведения (или 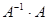), не лежащий на главной диагонали, равен сумме произведений элементов одной строки (или столбца) матрицы А на алгебраические дополнения к элементам друго столбца и, следовательно, равен 0 (как определитель с двумя равными столбцами). Элементы, стоящие на главной диагонали, равны Таким образом,

= . Теорема доказана.

Замечание. Сформулируем еще раз способ вычисления обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель.

Пример.

Найдем матрицу, обратную к

следовательно, матрица А невырожденная. Найдем алгебраические дополнения к ее элементам:

Не забудем, что алгебраические дополнения к элементам строки матрицы А образуют в обратной матрице столбец с тем же номером. Итак, Можно убедиться, что найденная матрица действительно удовлетворяет определению 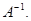Найдем

Тот же результат получим и при перемножении в обратном порядке.

Билет 4.

Ответ: Линейным уравнением называется уравнение вида

(2.1)

где 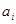и b – числа, 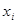- неизвестные.

Таким образом, в левой части линейного уравнения стоит линейная комбинация неизвестных, а в правой – число.

Системой линейных уравнений (линейной системой) называется система вида

(2.2)

где , - числа, - неизвестные, n – число неизвестных, m – число уравнений.

Решением линейной системы называется набор чисел

которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.

Не нашли, что искали? Воспользуйтесь поиском: