Математическая модель.

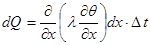(7.1)

С другой стороны, согласно закону сохранения энергий,

(7.2)

Левые части (7.1) и (7.2) равны, поэтому

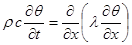
где ρ – плотность грунта [кг/м³];

с – массовая теплоемкость грунта [кдж/кг.град];

λ – коэффициент теплопроводности грунта [вт/м·град.].

При х = 0 задается температура 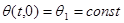. На поверхности земли происходит конвективный теплообмен между поверхностью тела и окружающей средой (воздух).

В основу изучения конвективного теплообмена положен закон Ньютона-Рихмана

где q – плотность теплового потока, вт/м²;

θ₀ – температура воздуха, ⁰С;

θ_гр – температура поверхности грунта, ⁰С;

α – коэффициент теплоотдачи, вт/(м²·град);

Согласно закону сохранения энергии, количество теплоты, отдаваемый единицей поверхности тела окружающей среде за единицу времени вследствие теплоотдачи, должно быть равно теплоте, которая путем теплопроводности подводится к единице поверхности в единицу времени со стороны внутренних частей тела, т.е.

(7.3)

Равенство (7.3) является математической формулировкой граничного условия третьего рода; оно является действительной для каждого момента времени t.

называется граничным условием первого рода.

Получена задача: найти решение нестационарного параболического уравнения со смешанными граничными условиями, т.е.

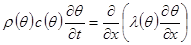(7.4)

θ(t,0) = θ₁ = const (7.5)

(7.6)

(7.7)

Теорема 1. При определенных условиях на ρ(θ), с(θ) и λ(θ) задача (7.4) - (7.7) имеет единственное решение.