Объем параллелепипеда

Если параллелепипед построен на приведенных к общему началу векторах , а , , , - радиус-векторы его соответствующих вершин то объем параллелепипеда

В координатах

12. Прикладные задачи векторного анализа: Площадь тетраэдра.
13. Прикладные задачи векторного анализа: Площадь треугольника

14. Прикладные задачи векторного анализа: Площадь параллелограмма
По определению векторного произведения двух векторов модуль векторного произведения равен площади параллелограмма, построенного на этих векторах. Поэтому для решения задачи найдем сначала векторное произведение 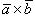, а потом его модуль. Согласно

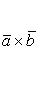
имеем

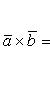
а модуль

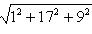
Искомая площадь параллелограмма

S = 19,26 кв. ед.

Замечание.

Векторное произведение 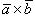можно было сразу определить по формуле

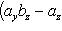
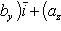
в которой следует взять

a_x = 5; a_y = -4; a_z = 7;

b_x = 1; b_y = 1; b_z = -2.

15. Прямая на плоскости. Угол между двумя прямыми.
Прямая — одно из основных понятий геометрии.

При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.

Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

16. Уравнение прямой.
Общее уравнение прямой линии на плоскости в декартовых координатах:

где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A, B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде:

Не нашли, что искали? Воспользуйтесь поиском: