
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Общее уравнение кривых второго порядка.
Общее уравнение кривой можно записать в матричном виде

19. Плоскость. Уравнение плоскости.
Пло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
• Общее уравнение (полное) плоскости

где 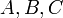 и
и  — постоянные, причём
— постоянные, причём  и
и 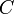 одновременно не равны нулю; в векторной форме:
одновременно не равны нулю; в векторной форме:

где 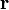 — радиус-вектор точки
— радиус-вектор точки  , вектор
, вектор  перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора
перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора  :
:



Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При  плоскость проходит через начало координат, при
плоскость проходит через начало координат, при 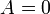 (или
(или  ,
,  ) П. параллельна оси
) П. параллельна оси  (соответственно
(соответственно  или
или  ). При
). При 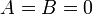 (
(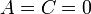 , или
, или  ) плоскость параллельна плоскости
) плоскость параллельна плоскости  (соответственно
(соответственно 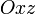 или
или  ).
).
• Уравнение плоскости в отрезках:

где 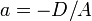 ,
,  ,
,  — отрезки, отсекаемые плоскостью на осях
— отрезки, отсекаемые плоскостью на осях  и
и  .
.
• Уравнение плоскости, проходящей через точку  перпендикулярно вектору нормали
перпендикулярно вектору нормали  :
:

в векторной форме:

• Уравнение плоскости, проходящей через три заданные точки  , не лежащие на одной прямой:
, не лежащие на одной прямой:

(смешанное произведение векторов), иначе

• Нормальное (нормированное) уравнение плоскости

в векторной форме:

где 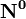 - единичный вектор,
- единичный вектор, 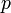 — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
— расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
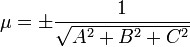
(знаки  и
и  противоположны).
противоположны).
20. Взаимное расположение двух плоскостей. Угол между двумя плоскостями.
Взаимное расположение двух плоскостей
Если 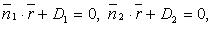 , то они:
, то они:
1) пересекаются 
2) параллельны (но не совпадают) 
3) совпадают 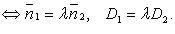
Если плоскости заданы уравнениями  и
и  то случаи 1 - 3 имеют месло, когда:
то случаи 1 - 3 имеют месло, когда:
1) 
2) 
3) 
Угол между плоскостями
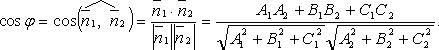
21. Прямая в пространстве. Уравнение прямой в пространстве.
Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.
Итак, если уравнения двух непараллельных плоскостей -- 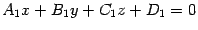 и
и 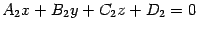 , то прямая, являющаяся их линией пересечения, задается системой уравнений
, то прямая, являющаяся их линией пересечения, задается системой уравнений
| (11.11) |
И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.
22. Взаимное расположение прямой и плоскости.
Прямая и плоскость в пространстве могут:
• а) не иметь общих точек;
• б) иметь ровно одну общую точку;
• в) иметь хотя бы две общие точки.

На рис. 30 изображены все эти возможности.
В случае а) прямая b параллельна плоскости  : b ||
: b ||  .
.
В случае б) прямая l пересекает плоскость  в одной точке О; l
в одной точке О; l 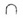
 = О.
= О.
В случае в) прямая а принадлежит плоскости  :
: 
 а или а
а или а 
 .
.
Теорема. Если прямая b параллельна хотя бы одной прямой а, принадлежащей плоскости  , то прямая параллельна плоскости
, то прямая параллельна плоскости  .
.
Предположим, что прямая m пересекает плоскость  в точке Q.Если m перпендикулярна каждой прямой плоскости
в точке Q.Если m перпендикулярна каждой прямой плоскости  , проходящей через точку Q, то прямая m называется перпендикулярной к плоскости
, проходящей через точку Q, то прямая m называется перпендикулярной к плоскости  .
.
Трамвайные рельсы иллюстрируют принадлежность прямых плоскости земли. Линии электропередачи параллельны плоскости земли, а стволы деревьев могут служить примерами прямых, пересекающих поверхность земли, некоторые перпендикулярные плоскости земли, другие — не перпендикулярные (наклонные).
23. Предел функции, свойства Раскрытие неопределённостей вида (бесконечность/бесконечность).
Свойства предела функции
1. Для того, чтобы число А было пределом f(x) при x->a, необходимо и достаточно, чтобы эта функция была представима в виде f(x)=A+альфа(х), где альфа(х) – бесконечно малая.
2. Предел постоянной величины равен самой постоянной. Lim C, x->a = C.
3. Если f(x)>= 0 (f(x)<=0) в некоторой окрестности точки а, кроме самой точки а, и в этой точке имеет предел, то предел lim f(x), x->a >=0 (lim f(x) x->a, <=0)
4. Если функции f1(x), f2(x) имеют пределы в точке а, то и их сумма, произведение и частное имеет пределы, причем lim (f1(x)+f2(x)), x->a=lim f1(x), x->a+lim f2(x), x->a, так же с произведением и частным
5. Если f(x) имеет предел в точке а, то lim (f(x))^n, x->a = (lim f(x), x->a)^n, где n – натуральное число
6. Постоянный множитель можно выносить за знак предела. Lim cf(x), x->a = cLim f(x), x->a.
7. Если для функций f(x), f1(x), f2(x) в некоторой окрестности в точке а выполняется неравенство f1(x)<=f(x)<=f2(x) и предел lim f1(x), x->a=lim f2(x), x->a=A, то lim f(x), x->a = A.
8. Lim c^x, x->б = бесконечности, если c>1 и 0, если 0<c<1.
Неопределенность вида бесконечность на бесконечность
Разделить все на х в наивысшей степени, учитывая уменьшение степени в корне.
Lim(x->0) sin 5x/sin3x = [0/0]=lim(x->0) x sin5x/x sin3x = lim(x->0) sin5x/x*lim(x->0) x/sin3x=lim(x->0) 5sin5x/5x*lim 3sin3x/3x)=5/3
Lim(x-unl) (1+1/x)x=e;
1/x=a=>x=1/a, a->0
Lim(a-0) (1+a)1/2=e
Lim(x-0) (loga(1+x))/x = lim(x-0) 1/x*loga(1+x)=lim(x-0) loga(1+x)1/x=logalim(x-0)(1+x)1/x=logae
Lim(x-0) ln(1+x)/x=ln e=1
Lim(x-0) ax-1/x=|ax-1=t;ax=t+1;ln ax=ln(t+1)
Не нашли, что искали? Воспользуйтесь поиском: