Тангенс угла наклона касательной прямой

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒

Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Основная статья: Касательная прямая

Если функция имеет конечную производную в точке x ₀, то в окрестности U (x ₀) её можно приблизить линейной функцией

Функция f_l называется касательной к f в точке x ₀. Число является угловым коэффициентом или тангенсом угла наклона касательной прямой.

[править] Скорость изменения функции

Пусть s = s (t) — закон прямолинейного движения. Тогда v (t ₀) = s '(t ₀) выражает мгновенную скорость движения в момент времени t ₀. Вторая производная a (t ₀) = s ''(t ₀) выражает мгновенное ускорение в момент времени t ₀.

Вообще производная функции y = f (x) в точке x ₀ выражает скорость изменения функции в точке x ₀, то есть скорость протекания процесса, описанного зависимостью y = f (x).

28. Правила дифференцирования функций. Таблица производных основных функций.

(частный случай формулы Лейбница)

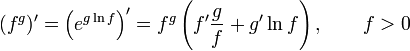
— Правило дифференцирования сложной функции

Производные простых функций

•

•

•

Вывод [показать]

• когда и определены,

Вывод [показать]

•

Вывод [показать]

•

•

•

•

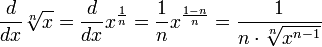
⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: