Производная параметрически заданной функции.

В зависимости от правила, устанавливающего зависимость между множествами значений величин x и y, различают несколько способов задания функции. Наиболее привычным является представление функции в явном виде . Однако, в некоторых случаях удобно описывать функциональную зависимость множеством пар значений (x; y), которые вычисляются для каждого значения параметра t из промежутка (a; b). К примеру, все пары значени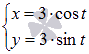й при 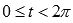задают окружность с центром в начале координат радиуса 3.

Определение параметрически заданной функции.

Таким образом, если определены при и существует обратная функция для 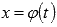, то говорят о параметрическом задании функции .

При исследовании параметрически заданной функции иногда приходится находить ее производную по аргументу x. В этой статье мы выведем формулу производной параметрически заданной функции , также остановимся на производной второго и n-ого порядка.

Вывод формулы производной параметрически заданной функции.

Пусть определены и дифференцируемы при , причем и 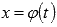имеет обратную функцию .

Сначала переходим от параметрического задания к явному. При этом получаем сложную функцию , аргументом которой является x.
По правилу нахождения производной сложной функции имеем: 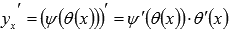. Так как и 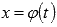обратные функции, то по формуле производной обратной функции , поэтому .

Не нашли, что искали? Воспользуйтесь поиском: