Производные высших порядков.

Пусть y = f (x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде

Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:

Производные более высокого порядка (если они существуют), определяются как

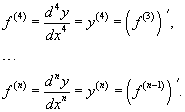
Для нахождения производных высшего порядка можно использовать следующие формулы:

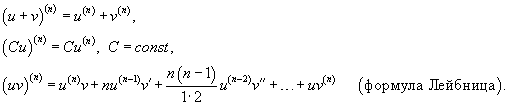
В частности, для производной второго и третьего порядка формула Лейбница принимает вид

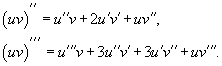
Пример 1

Найти y'', если .

Решение.

Возьмем первую производную дифференцируя функцию как произведение.

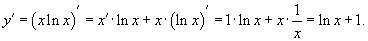
Теперь найдем производную второго порядка

Пример 2

Вычислить y'' для параболы .

Решение.

Дифференцируя как неявную функцию, имеем

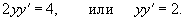
Дифференцируя еще раз и используя правило для производной произведения, получаем

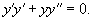
Умножим обе части на y ²:

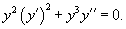
Поскольку yy' = 2, и следовательно, (yy')² = 4, то последнее уравнение записывается в виде:

Отсюда следует, что

Пример 3

Найти все производные функции .

Решение.

Пусть u = e ^x и v = x ². Тогда

Легко устанавливаются общие формулы для производных n -порядка:

Используя формулу Лейбница

получаем

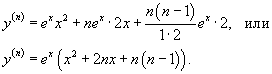
Пример 4

Определить все производные синуса.

Решение.

Вычислим несколько первых производных:

Очевидно, что производная n- го порядка выражается формулой

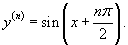
Пример 5

Найти все производные функции .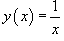

Решение.

Аналогично предыдущему примеру, найдем сначала несколько первых производных.

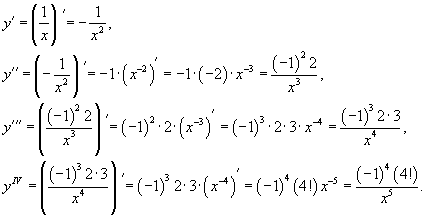
Этого достаточно, чтобы обнаружить общий "паттерн":

Не нашли, что искали? Воспользуйтесь поиском: