Отношение бесконечно малых

Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида .

Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a, мы можем непрерывным образом их доопределить в этой точке: пусть f (a) = g (a) = 0. Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку теорему Коши. По этой теореме получим:

,

но f (a) = g (a) = 0, поэтому .

Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим:

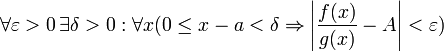для конечного предела и

для бесконечного,

что является определением предела отношения функций.

[править] Отношение бесконечно больших

Докажем теорему для неопределённостей вида .

Пусть, для начала, предел отношения производных конечен и равен A. Тогда, при стремлении x к a справа, это отношение можно записать как A + α, где α — O(1). Запишем это условие:

.

Зафиксируем t из отрезка и применим теорему Коши ко всем x из отрезка :

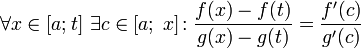, что можно привести к следующему виду:

.

Для x, достаточно близких к a, выражение имеет смысл; предел первого множителя правой части равен единице (так как f (t) и g (t) — константы, а f (x) и g (x) стремятся к бесконечности). Значит, этот множитель равен 1 + β, где β — бесконечно малая функция при стремлении x к a справа. Выпишем определение этого факта, используя то же значение ε, что и в определении для α:

.

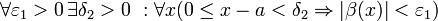Получили, что отношение функций представимо в виде (1 + β)(A + α), и . По любому данному ε можно найти такое ε₁, чтобы модуль разности отношения функций и A был меньше ε, значит, предел отношения функций действительно равен A.

Если же предел A бесконечен (допустим, он равен плюс бесконечности), то

.

В определении β будем брать ; первый множитель правой части будет больше 1/2 при x, достаточно близких к a, а тогда .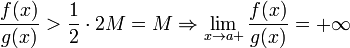

Для других баз доказательства аналогичны приведённым

34. Исследование функции с помощью производной.

еорема. 1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f′(x) ≥ 0.

2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f′(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].

Доказательство.

1) Если функция f(x) возрастает, то f(x + Äx) > f(x) при Äx>0 и f(x + Äx) < f(x) при Äх<0,

тогда:

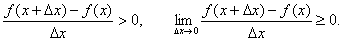
2) Пусть f′(x)>0 для любых точек х₁ и х₂, принадлежащих отрезку [a, b], причем x₁<x₂.

Тогда по теореме Лагранжа: f(x₂) – f(x₁) = f′(å)(x₂ – x₁), x₁ < å < x₂

По условию f′(å)>0, следовательно, f(x₂) – f(x₁) >0, т.е. функция f(x) возрастает.

Теорема доказана.

Аналогично можно сделать вывод о том, что если функция f(x) убывает на отрезке [a, b], то f′(x)≤0 на этом отрезке. Если f′(x)<0 в промежутке (a, b), то f(x) убывает на отрезке [a, b].

Конечно, данное утверждение справедливо, если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b).

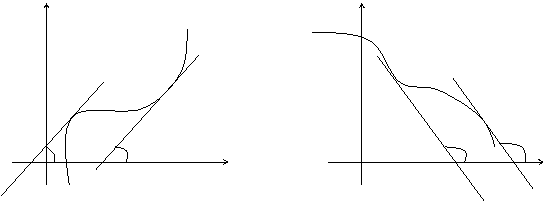Доказанную выше теорему можно проиллюстрировать геометрически:

y y

ϕ ϕ ϕ ϕ

x x

Точки экстремума.

Определение. Функция f(x) имеет в точке х₁ максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х₁. Функция f(x) имеет в точке х₂ минимум, если f(x₂ +Äx) > f(x₂) при любом Äх (Äх может быть и отрицательным).

Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.

Определение. Точки максимума и минимума функции называются точками экстремума.

Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х₁ и точка х₁ является точкой экстремума, то производная функции обращается в нуль в этой точке.

Доказательство. Предположим, что функция f(x) имеет в точке х = х₁ максимум.

Тогда при достаточно малых положительных Äх>0 верно неравенство:

, т.е.

Тогда

По определению:

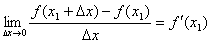
Т.е. если Äх→0, но Äх<0, то f′(x₁) ≥ 0, а если Äх→0, но Äх>0, то f′(x₁) ≤ 0.

А возможно это только в том случае, если при Äх→0 f′(x₁) = 0.

Для случая, если функция f(x) имеет в точке х₂ минимум теорема доказывается аналогично.

Теорема доказана.

Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х³, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.

Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.

Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно.

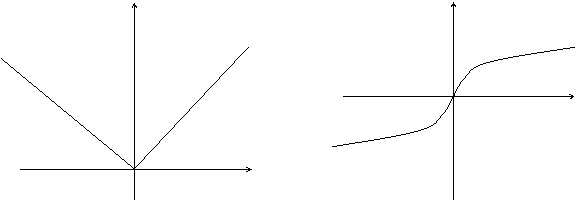
Пример: f(x) = ⎮x⎮ Пример: f(x) =

y y

x

x

В точке х = 0 функция имеет минимум, но В точке х = 0 функция не имеет ни

не имеет производной. максимума, ни минимума, ни произ-

водной.

Вообще говоря, функция f(x) может иметь экстремум в точках, где производная не существует или равна нулю.

Теорема. (Достаточные условия существования экстремума)

Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х₁, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х₁).

Если при переходе через точку х₁ слева направо производная функции f′(x) меняет знак с “+” на “-“, то в точке х = х₁ функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.

Доказательство.

Пусть

По теореме Лагранжа: f(x) – f(x₁) = f′(å)(x – x₁), где x < å < x₁.

Тогда: 1) Если х < x₁, то å < x₁; f′(å)>0; f′(å)(x – x₁)<0, следовательно

f(x) – f(x₁)<0 или f(x) < f(x₁).

2) Если х > x₁, то å > x₁ f′(å)<0; f′(å)(x – x₁)<0, следовательно

f(x) – f(x₁)<0 или f(x) < f(x₁).

Т. к. ответы совпадают, то можно сказать, что f(x) < f(x₁) в любых точках вблизи х₁, т.е. х₁ – точка максимума.

Доказательство теоремы для точки минимума производится аналогично.

Теорема доказана.

На основе вышесказанного можно выработать единый порядок действий при нахождении наибольшего и наименьшего значения функции на отрезке:

1) Найти критические точки функции.

2) Найти значения функции в критических точках.

3) Найти значения функции на концах отрезка.

4) Выбрать среди полученных значений наибольшее и наименьшее.

35. Асимптоты графика функции.
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

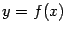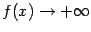Определение: Вертикальной асимптотой графика функции называется вертикальная прямая , если или при каком-либо из условий: , , 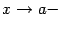. Заметим, что мы при этом не требуем, чтобы точка 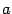принадлежала области определения функции 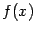, однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: или , где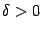

Не нашли, что искали? Воспользуйтесь поиском: