
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Сравнение бесконечно малых функций
Пусть a(x,b(x) – бесконечно малые ф-ции при х->a
Тогда
1. Lim(x->a) a(x)/b(x)=0 => a(x) – бесконечно малая более высокого порядка, чем b(x)
2. Lim(x->a) a(x)/b(x) =c <>0=> a и b – бесконечно малые функции одного порядка
3. Lim(x->a) a(x)/b(x) = 1 => a u b – эквивалентные бесконечно малые функции
4. Lim(x->a) d(x)/bn(x) = c <>0 => a – бесконечно малая функция н-ного порядка относительно b(x)
Cos2x=1-2sin2x
Теорема: если б.м. а(х) эквивалентна а1(х) и b(x) ~b1(x) и lim(x->a)a(x)/b(x) => lim(x->a)a1(x)/b1(x)
1. Sin kx ~ kx
2. Tg kx ~kx
3. Arcsin kx ~ kx
4. Arctg kx ~kx
5. Ekx-1 ~ kx
6. Akx~kx ln a
7. Ln |1+kx|~kx
8. 1-cos kx ~kx2/2
23. Предел функции, теоремы о пределах. Неопределённость вида 0/0.
• Бесконечно большие и бесконечно малые.
Функция f (x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение ä > 0, что для всех x удовлетворяющих неравенству | x − a | < ä имеет место неравенство | f (x)| > M.
lim x → a =∞
• Функция ограниченная при x → a.
• Функция ограниченная при x → ∞.
• Теорема. Если lim x → a f (x)= b, то функция f (x) ограниченная при x → a.
• Бесконечно малые и их свойства. lim x → a á(x)=0
Теорема. 1. Если f (x)= b +á, где á - б.м. при x → a, то lim x → a f (x)= b и обратно, если lim x → a f (x)= b, то можно записать f (x)= b +á(x).
Теорема. 2. Если lim x → a á(x)=0 и á(x) ≠ 0, то 1/á→ ∞.
Теорема. 3. Сумма конечного числа б.м. есть б.м.
Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.
• Теоремы о пределах.
Теорема. 1. Предел суммы есть сумма пределов.
Теорема. 2. Предел произведения есть произведение пределов.
Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).
Теорема. 4. Если u (x) ≤ z (x) ≤ v (x), и lim x → a u (x)=lim x → a v (x)= b, то lim x → a z (x)= b. ("Теорема о двух милиционерах").
• Первый замечательный предел.
| 0.5sin(x) < 0.5 x < 0.5tg(x) |
| lim x → 0 sin(x) x =1. |
• Второй замечательный предел.
Переменная величина
| ⎛ ⎝ 1+ 1 n ⎞ ⎠ n |
при n → ∞ имеет предел, заключенный между 2 и 3.
В данной работе мы рассмотрим неопределенность вида  для функции
для функции 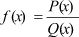 . Для нахождения предела функции мы применяем метод преобразования, метод замены и определение бесконечно малых величин.
. Для нахождения предела функции мы применяем метод преобразования, метод замены и определение бесконечно малых величин.
Пусть требуется найти предел дроби
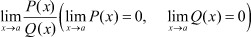 (1)
(1)
где P(x) и Q(x) функции определенные в окрестности предельного аргумента a, но в самом предельном значении обращаются в ноль.
Теорема 1. Пусть число a для многочлена n-й степени P(x) = Pn(x) является k кратным решением, а для многочлена m-й степени Q(x) = Qn(x) является r кратным решением, тогда
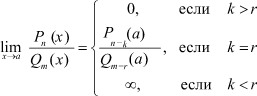 (2)
(2)
где Pn-k(a) и Qm-r(a) значения соответствующих многочленов Pn-k(x) и Qm-r(x) в точке x = a.
Доказательство. Так как, число a является решением многочленов Pn(x) и Qm(x), то их в любое время можно представить в виде:

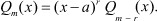
Тогда
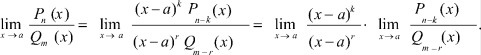 (3)
(3)
Биномы (x - a)k и (x - a)r в окрестности точки x = a бесконечно малы, а их основания эквивалентные бесконечно малые.
Отсюда
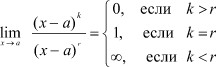
Полагаясь на последнее равенство, можно из (3) предела получить формулу (2).
Не нашли, что искали? Воспользуйтесь поиском: